Seien K ein Körper, V ein endlich-dimensionaler K-Vektorraum und α ∈ End(V ).
Sei K := R, V := R5 und α bezüglich der geordneten Standardbasis ^B gegeben durch
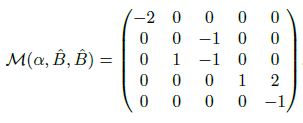
Zeigen Sie, dass 1;-1 und -2 Eigenwerte von α sind und finden Sie jeweils einen Eigenvektor!
Schreiben Sie dann V als direkte Summe α-zyklischer Teilräume.
Für den ersten Teil, habe ich die Zeilen 2 und 3 miteinander vertauscht und somit sieht man die EW auf der diagonalen liegen.
Für die Eigenvektoren habe ich für EW(-2) = (1,0,0,0,0) EW(1) = (0,0,0,1,0) und EW(-1) = (0,0,0,-1,1) ermittelt. Nun weiss ich
aber mit der letzten Teilaufgabe überhaupt nicht weiter, würde mich über eure Hilfe sehr freuen. ;)