Sekantenberechnung im Koordinatensystem: fS1(x) = 14/9x+28/9 und fS2(x)= -2,2x+1,6

Question

Ich habbe zwei Sekanten im Koordinatensystem. Die Gleichung beider Sekanten habe ich bereits ausgerechnet:

fS1(x) = 14/9x+28/9 und fS2(x)= -2,2x+1,6

Diese habe ich in ein gemeinsames Koordinatensystem eingezeichnet. Diese Sekanten schneiden sich in einem Punkt und bilden mit der X-Achse ein Dreieck. Von diesem Dreieck muss ich nun den Flächeninhalt berechnen.

Wie mache ich das ? Könnte mir das jemand erklären ? Ich weiß nämlich nicht, woher ich die jeweilige Länge der Seiten herbekomme, da ich nicht weiß , wie ich das Ausrechnen soll.

 

Answer 1

 

Du hast ja jetzt ein Dreieck gegeben, welches ungefähr so aussieht:

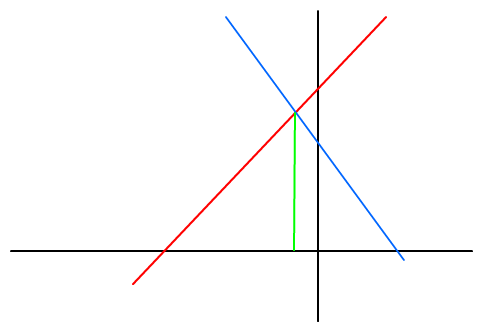
rot = fS₁(x)

blau = fS₂(x)

 

Der Flächeninhalt des links vom grünen Strich liegenden Teildreiecks kann dann so berechnet werden: 

(x-Koordinate des Schnittpunkts der beiden Tangenten minus Nullstelle von fS₁) * (y-Koordinate des Schnittpunkts der beiden Tangenten) / 2

 

Analog der Flächeninhalt des rechts vom grünen Strich liegenden Teildreiecks:

(Nullstelle von fS₂ minus x-Koordinate des Schnittpunktes der beiden Tangenten) * (y-Koordinate des Schnittpunkts der beiden Tangenten) / 2 

 

Dann diese beiden Teilflächen addieren. 

 

Mir ist eben eingefallen: 

Noch einfacher und schneller geht: 

(Nullstelle von fS₂ - Nullstelle von fS₁) * (y-Koordinate des Schnittpunktes der beiden Tangenten) / 2

Breite                                                           *                                            Höhe                                          / 2

 

Alles klar?

Besten Gruß

Answer 2

Nun, die Schnittpunkte der Sekanten mit der x-Achse erhältst du, indem du die Nullstellen der Sekanten berechnest. Setze also die Funktionsterme der Sekantengleichungen jeweils gleich Null und löse nach x auf. Die y-Koordinate eines Punktes, der auf der x-Achse liegt, ist immer gleich Null.

Die x-Koordinate des Schnittpunktes der beiden Sekanten findest du, indem du die Funktionsterme der Sekantengleichungen einander gleichsetzt und nach x auflöst. Die y-Koordinate dieses Punktes findest du, indem du die berechnete x-Koordinate in eine der beiden Sekantengleichungen einsetzt und ihren Wert ausrechnest.

Kommst du nun erst einmal selber klar?