Gleichungen im Koordinatensystem y=2x+1

Question

brauche nochmals eure Hilfe.

Gleichungen

g1:   y = 2x+1

g2:   3x+y=1

g3:   x+2y=17

g4:   -4x+2y=8

a) Zeichnen Sie die 4 Geraden in ein Koordinatensystem. Suchen und berechnen Sie alle Schnittpunkte, die auftreten können.

b) Bennen Sie den Schnittpunkt der Gerade g1 und g2 mit S12 und entsprechend alle weiteren Schnittpunkte.

c) Wie lautet die Gleichung der Verbindungsgeraden S12 mit S34 in der Normalform.

Vielen, vielen Dank.

Comments

Welche dieser Aufgaben kannst du denn nicht selber bearbeiten? Wo hast du Probleme?

---

Ich weiß nicht, muss ich die Formeln erst umrechnen. Dann ist mir zum Teil die zeichnerische Darstellung im Koordinatensystem nicht logisch.

Wäre echt super, wenn mir da jemand helfen kann.

Danke.

---

Du solltest alle Gleichungen nach y auflösen und dann die Graphen einzeichnen, wie man das im Video hier sieht:

https://www.matheretter.de/wiki/lineare-funktionen

Answer 1

Du musst die Formeln nicht unbedingt erst umrechnen, also nach y auflösen. Aber es macht die Sache einfacher.

Also:

Auflösen nach y ergibt:

g1: y = 2 x + 1

g2: y = - 3 x + 1

g3: y = - 0,5 x + 8,5

g4: y = 2 x + 4

Nun kannst du zu jeder der Geraden deren Steigung (Faktor vor dem x) und deren y-Achsenabschnitt (Summand ohne x) ablesen. Damit hast du für jede Gerade genügend Informationen um sie in ein Koordinatensystem zu zeichnen.

Das sollte dann so aussehen:

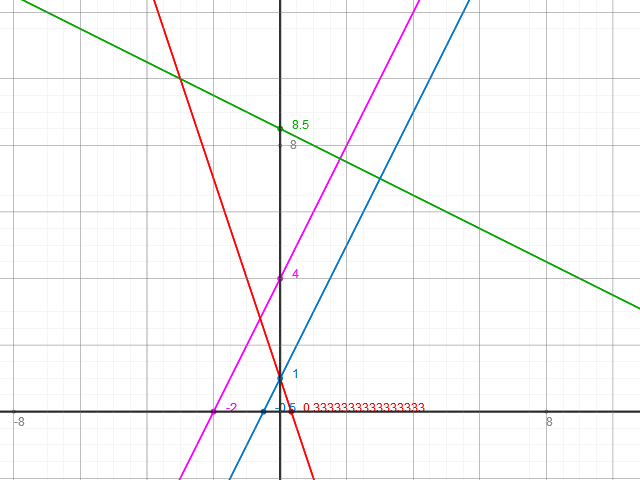
Nun kannst du die Schnittpunkte sehen und auch berechnen, indem du jeweils die Gleichungen der beiden an einem Schittpunkt beteiligten Geraden gleichsetzt und nach x auflöst.

 

c)

Der Punkt S12, also der Schnittpunkt der Geraden g1 mit der Geraden g2, hat die Koordinaten S12 ( 0 | 1 )

Die Koordinaten des Punktes S34, also des Schnittpunktes der Geraden g3 mit der Geraden g4, kann man aus der Zeichung nicht ablesen, er muss berechnet werden, also:

g3 = g4

<=> - 0,5 x + 8,5 = 2 x + 4 | + 0,5 x

<=> 8,5 = 2,5 x + 4 | - 4

<=> 2,5 x = 4,5 | / 2,5

<=> x = 1,8

Die y-Koordinate ergibt sich durch Einsetzen in eine der beiden ursprünglichen Gleichungen, ich nehme g4:

y = 2 * 1,8 + 4 = 7,6

Also hat der Schnittpunkt S34, also der Schnittpunkt der Geraden g3 mit der Geraden g4, die

Koordinaten S34 ( 1,8 | 7,6 )

 

Nuin hast du zwei Punkte und kannst die Geradengleichung bestimmen. Schaffst du das?

Comments

Danke, das war sehr hilfreich. Denke das bekomme ich hin. Nochmals danke

---

Danke, das war sehr hilfreich. Denke das bekomme ich hin. Nochmals danke. Nur beim zeichnen der gerade wie kommst du auf g1=-0, 5 und g2=0,333. Ich hab plus und minus gerade anderst rum. Auch -17 statt 17.

---

Ich kann deine Rückfrage kaum nachvollziehen. Insbesondere sehe ich nicht,

Deshalb schreibe ich die Umformungen aller Geraden noch einmal auf:

g1:

Ist schon in der gewünschten Form

g2:

3 x + y = 1 

<=> y = 1 - 3 x

Umordnen, damit der Term mit x zuerst dasteht:

<=> y = - 3 x + 1

g3:

x + 2 y  = 17

<=> 2 y = 17 - x

<=> y = 8,5 - 0,5 x

<=> y = - 0,5 x + 8,5

g4:

- 4 x + 2 y = 8

<=> 2 y = 8 + 4 x

<=> y = 4 + 2 x

<=> y = 2 x + 4

 

Falls du die Werte meinst, die in dem Diagramm auf der x-Achse stehen (-2 , - 0,5 und 0,333... )  - das sind die Nullstellen der Geraden g1, g2 und g4), also diejenigen Werte x, für die die jeweilige Geradengleichung den Wert 0 liefert. Die aber habe gar nicht ich berechnet, sondern die hat das Zeichenprogramm dort eingefügt.