Lineares Optimierungsproblem lösen

Question

gegeben ist eine Zielfunktion unter folgenden Bedingungen:

z = 20x + 30y, wobei x ≥ 0, y ≥ 0, 7x + 19y ≤ 1596, 4x + 4y ≤ 720

a) Gebe die Koordinaten der anderen drei Ecken des Gebiets an! 

b) In welchem Punkt erreicht die Zielfunktion ihren max. Wert?

c) Wie groß ist der maximale Wert?

Answer 1

Hallo Blackmaster 3,

gesucht  graphische  Lösung:

Zeichne die Geraden g:  7x+19y = 1596  ,  h  = 4x+4y = 720

Du erhältst deren Schnittpunkte mit den Achsen durch Nullsetzen einer Koordinate und Berechnung der anderen.

Das eingezeichnete zulässige Gebiet liegt im 1. Quadranten unterhalb von g und h einschließlich der Geraden selbst.

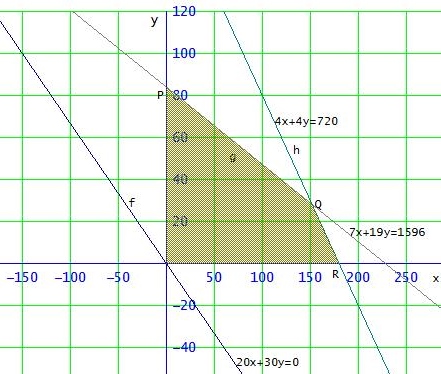
Die Zielfunktion  z = 20x + 30y   ist für z=0 eingezeichnet.

Diese musst du soweit wie möglich parallel nach oben verschieben, so dass sie mindestens noch einen Punkt mit dem zulässigen Gebiet gemeinsam hat   [hier Q] .

Der y-Wert des Schnittpunkts dieser Parallelen ist dann der Maximalwert der Zielfunktion.

--------_max

Rechnerisch  ergibt sich der Schnittpunkt von g und h zu  Q(152|28)

Zielfunktion:   y = -2/3 x + z/30 

Optimierungsgerade  y = -2/3 * (x - 152) + 28  = -2/3 x + 388/3 

→  z_max = 3880 

Gruß Wolfgang

Comments

Danke, das Prinzip ist mir nun ersichtlich.

Wie beschreibe ich denn rechnerisch den Punkt R und P? ablesen reicht in der Klausur nicht um einen Punkt zu bekommen, muss ich die Gerade wieder gleichsetzen? so wie bei dem Punkt Q?

---

Für  P musst du in   7x+19y = 1596   x=0 setzen und y ausrechnen

Für  R  musst du in  4x+4y = 720   y=0 setzen und x ausrechnen