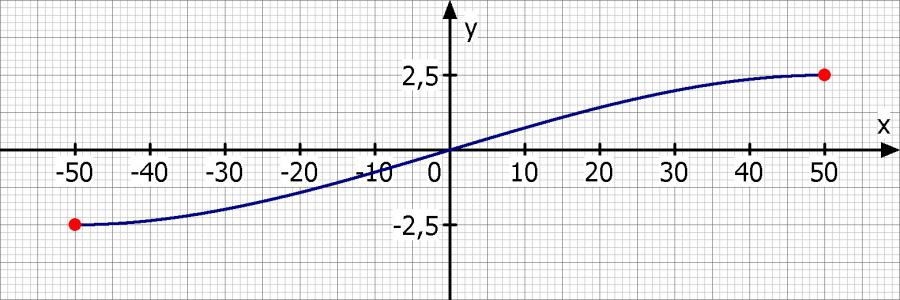
Weil die eine Funktion suchen, die punktsymmetrisch zum Koordinatenursprung ist. Dadurch hat man nur ungerade Exponenten von x.
f(x) = ax^3 + bx
Bedingungen
f(50) = 2.5
f'(50) = 0
Die Gleichungen
125000·a + 50·b = 5/2
7500·a + b = 0
Die Lösung des LGS ist a = -1/100000 ∧ b = 3/40
Damit würde die Funktion wie folgt lauten:
f(x) = - 1/100000·x^3 + 3/40·x
Die Trassierung in diesem einfachen Fall erfolgt aber nicht krümmungssprungfrei. Ich glaube darauf wird im weiteren Aufgabenverlauf auch hingewiesen.