Trassierung: f(x)=x und g(x)=-x sollen im Bereich -1 bis 1 verbunden werden.

Question

Die rechtwinklige Ecke einer Straße soll durch einen Bogen ersetzt werden, um Unfallgefahren zu vermindern. Für die neue Straßenführung soll der Bogen ansetzen an die Straßen, die in einem lokalen Koordinatensystem in der Einheit km beschrieben werden durch f(x) = x für x ≥ 1 und g(x) = -x für x ≤ -1. Bestimmen Sie eine geeignete Funktion.

Ich verstehe die Aufgabe einfach nicht, schon allein die Aufgabestellung.

Answer 1

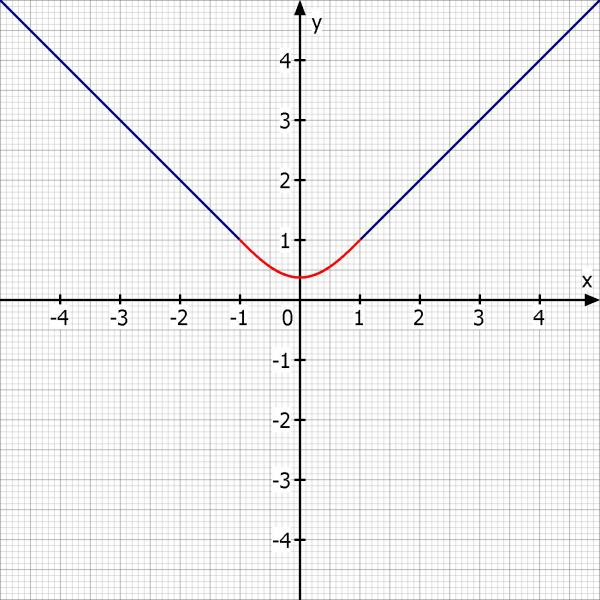
Das gehört zu den Trassierungsaufgaben

Gesucht ist z.B. eine ganzrationale Funktion die die beiden Straßenteile, knickfrei und krümmungsfrei verbindet.

 

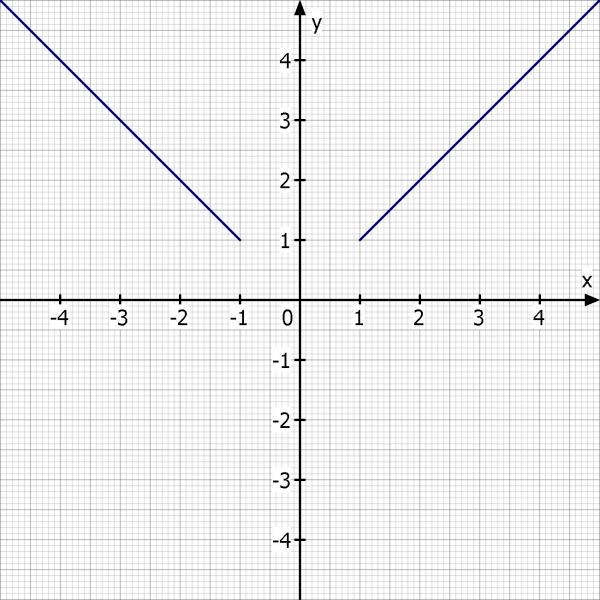
Die Bedingungen dafür sind:

Achsensymmetrisch
f(x) = ax^4 + bx^2 + c

f(1) = 1
f'(1) = 1
f''(1) = 0

Daraus resultieren die Gleichungen

a + b + c = 1
4·a + 2·b = 1
12·a + 2·b = 0

Die Lösung des LGS ist a = - 1/8 ∧ b = 3/4 ∧ c = 3/8

Die Funktion lautet daher

f(x) = - 1/8·x^4 + 3/4·x^2 + 3/8

Damit sieht das ganze dann so aus:

 

Comments

Manche Lehrer fordern nur das die Straße knickfrei verläuft. Dann könnte man das mit einer Funktion 2. Grades machen. Besser ist allerdings die Methode, das die Straße auch krümmungsfrei verläuft.

Krümmungsfrei soll bedeuten das es keine Krümmungssprünge gibt.
So könnte man rein Theoretisch die Kurve auch durch einen Kreisbogen modellieren. Allerdings wäre das dann nicht Krümmungsfrei.

---

@ Mathecoach:
Was spricht gegen eine Funktion 2. Grades (s.u.)?

Du hast schon von einem "Krümmungssprung" gesprochen, aber wenn man h(x) = 0,5x² + 0,5 von einem Plotter zeichnen lässt, sieht das ganz "smooth" aus :-)

---

Das die Übergänge einen Sprung im Krümmungsverhalten haben. Das heißt die Modellierte Funktion hat im Übergangspunkt eine andere Krümmung als die anschließende Straße.

Stell dir vor du bist für einen Fahradparkour auf dem Schulhof verantwortlich und entwirfst eine 8 aus zwei Kreisen.

Fährst du in dem einen Kreis hast du meinetwegen den Lenker immer links eingeschlagen. Willst du dann in den anderen Kreis fahren hast du ein Problem denn du müsstest das Lenkrad in der Übergrangsstelle herumreißen weil du im anderen Kreis immer einen Lenkereinschlag nach rechts hast. Man braucht also quasi hier auch einen Wendepunkt wo die Krümmung sich langsam ändert und nicht sprunghaft.

---

Schau dir eventuell mal den direkten Vergleich an:

Der grüne Graph gibt den etwas smootheren Übergang :) Man hat dort langsam Zeit in die Kurve hineinzulenken und langsam herauszulenken.

---

Danke, das verstehe ich. 

Aber würdest Du das hier eine sprunghafte Änderung der Krümmung bezeichnen?

---

O.k., dann hat sich mein letzter Kommentar erübrigt :-)

P.S. Wäre es dann nicht noch "smoother", wenn man mit einem symmetrischen Polynom 8. Grades arbeiten würde? Wo sind da die Grenzen? Oder fehlen dann ganz einfach Daten, um die Funktionsgleichung zu erstellen?

---

Ja. Denn die Parabel ist in jedem Punkt linksgekrümmt. Die geraden Straßen haben allerdings keine Krümmung. Daher wäre hier der Übergangspunkt nicht Krümmungsfrei bzw. hätte einen Krümmungssprung.

---

Aber auch bei Deiner Lösung, die zugegebenermaßen "weicher" ist, hast Du eine Linkskrümmung, nur halt nicht so stark :-)

---

Man geht in der Schulmathematik davon aus das es erstmal langt wenn sich die Krümmung allmählich ändert. Daher sind Übergänge knickfrei und krümmungssprungfrei zu entwerfen.
In wie weit da in der Praxis auch mit gerechnet wird weiß ich nicht. Da spielen vermutlich andere Dinge noch eine wichtigere Rolle.

---

Gut, beenden wir das hier.
Wenn man im Münsterland lebt wie ich, glaubt man ohnehin nicht, dass bei der Planung von Straßen irgendwelche mathematischen Methoden angewendet werden :-D

---

Also meine Funktion ist an den Übergabepunkten krümmungsfrei. Meine Funktion hat dort ja Wendepunkte.
Man lenkt also sanft in die Kurve hinein und wieder heraus. Man braucht keine hektischen Lenkerbewegungen um dem exakten Straßenverlauf zu folgen.

---

Bei Deinem direkten Vergleich oben würde ich persönlich aber lieber die rote Strecke als die grüne fahren; man tendiert doch - sofern es der Verkehr zulässt - auch eher dazu, eine Kurve zu schneiden als sie ganz weit auszufahren; Stichwort "Ideallinie".

---

Ja. Das macht man im allgemeinen damit man keine zu große Krümmung hat und dadurch schneller fahren kann.
Die Ideallinien haben daher immer eine möglichst kleine Krümmung verlaufen selber aber auch ohne Krümmungssprünge.

Angeblich soll man solche Krümmungssprünge bei Eisenbahntrassen spüren.

---

Wahrscheinlich hat jede Lösung ihre Vor- und Nachteile:
Mit Deiner Funktion geht man sanfter in die Kurve, bei meiner Funktion ist der Übergang von f(0,25) auf f(-0,25) weicher ...

Auf jeden Fall war es eine sehr interessante Diskussion.

Jetzt ist aber eine Bettlagerung angesagt: Gekrümmt oder nicht gekrümmt, das ist hierbei nicht die Frage :-D

---

Nur falls es dich interessiert. Bei der anderen Trassierungsaufgabe:

https://www.mathelounge.de/45946

Ist der einfache Ansatz auch einer der keine Krümmungsfreiheit an den Übergangspunkten voraussetzt.

Ich glaube die Aufgabe war mal Teil einer Hamburger Abiturprüfung. Sie kommt mir auf jedenfall sehr bekannt vor. Aber es werden ja auch immer Aufgaben auch von anderen abgewandelt.

Answer 2

Hi, 

was wir haben, sieht in etwa so aus: 

Jetzt sollen also die Punkte (-1|1) und (1|1) durch einen Bogen miteinander verbunden werden, damit die Verländerungen von f(x) und g(x) nicht im Ursprung rechtwinklig aufeinanderstoßen. 

Idee: 

Ich würde ausgehen von einer Funktion 2. Grades

h(x) = ax² + bx + c

h'(x) = 2ax + b

mit 

h(1) = 1

h(-1) = 1

h'(1) = 1

 

Es ergeben sich die folgenden Gleichungen: 

a + b + c = 1

a - b + c = 1

2a +b     = 1

a = 0,5

b = 0

c = 0,5

 

Und damit die Funktionsgleichung: 

g(x) = 0,5 * x² + 0,5

     

Besten Gruß

Comments

Nur noch einmal um die oben genannte Diskussion abzuschließen.
Beim Straßenbau ist auch die zweite Ableitung der Funktion wichtig. Diese gibt "quasi" an, wie das Lenkrad bewegt wird. D.h. ist ein Sprung in der zweiten Ableitung, müsste man um die Ideallinie zu fahren, das Lenkrad von der Mittelstellung zur Seite instantan "springen" lassen.

Ist die zweite Ableitung jedoch stetig, kann das Lenkrad eingedreht werden.

Deshalb ist die erste Lösung für den Strassenbau korrekt.
Muss aber ein 13 Klässler erstmal drauf kommen.