Also folgendes Problem haben wir. Also wir wollen so eine Diamantenform mit der Fläche 3m^2. Zusätzlich möchten wir natürlich auch die Materialkosten niedrig halten. (sonst gibt es unenedlich viele Lösungen) Da reicht es den Umfang zu betrachten.
U=2a+2b -> min (soll minimal werden)
Nebenbedingung ist A=3m^2
Jetzt müssen wir A nur mehr von a und b abhängig machen.
Ich habe den Diamanten in ein obenstehendes Trapez mit Höhe h und Seiten c,a,a,a und ein untenstehendes Dreieck mit Seiten b,b,c und Höhe hc zerlegt.
Gut allgemein gilt dann für den Flächeninhalt:
A=(c*hc)/2+(a+c)/2*h
Wie du schon gesagt hast wünschen wir uns einen Winkel von 90 Grad zwischen den Seiten b,b
Somit folgt dann mittels Pythagoras:
c=√(b^2+b^2)=b*√2
Jetzt betrachte ich folgendes Dreieck:
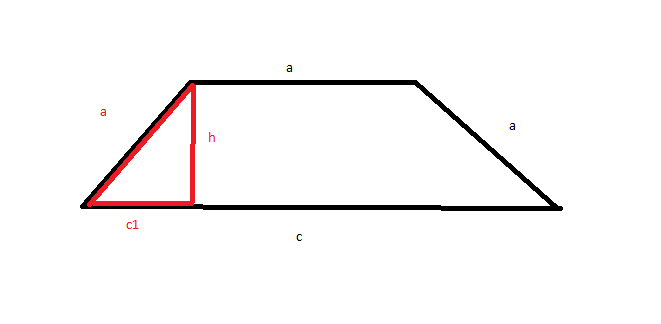
Wobei wir c1 als Hilfsvariable einführen. c1=(c-a)/2
So mit dieser Bezeichnung können wir uns jetzt h ausrechnen (wieder mittels Pythag. Lehrsatz):
h=√(a^2-c1^2)=√(a^2-((c-a)^2/4)=√(a^2-((b*√2-a)^2/4)
Um noch hc zu berechnen betrachten wir folgendes Dreieck:
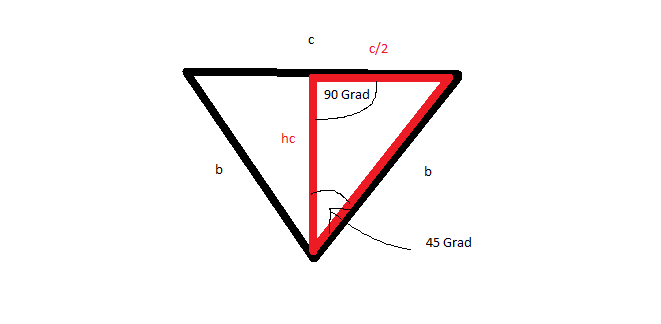
Da ist aber sofort klar das der letzte Winkel 45 Grad ist und somit muss hc =c/2 sein
und somit hc=(b*√2)/2
Jetzt gibt es das Minimierungsproblem zu lösen. Material minimal mit Nebenbedingung A=3m^2
A=(b*√2*(b*√2)/2)/2+(a+b*√2)/2*√(a^2-((b*√2-a)^2/4)
=b^2/2+(a+b*√2)/2*√(a^2-((b*√2-a)^2/4)=3
da sollte man jetzt auf a oder b ausdrücken (was ich grad echt nicht leicht finde) und in
U=2*a+2*b.
Danach hat man ein U(a) oder ein U(b). Dann sind folgende Schritte zu machen.
1) Ableiten
2) Nullstelle der Ableitung bestimmen.
3) Prüfen ob es eh ein Maximum ist. Indem man die Nullstelle in U(a) (oder U(b) einsetzt).
Ich mach jetzt mal Pause und schau ob ich dann noch weiter komm.