Integral bestimmen ohne Stammfunktion

Question

 könnt ihr mir bei der Aufgabe helfen?

Answer 1

Hallo HJ,

f(t)  =  t³ * cos(t) * ln(1+t^2)

f(-t)  =  (-t)^3 * cos(-t) * ln(1+(-t)^2)  =  - t³ * cos(t) * ln(1+t^2)  =  - f(t) 

Für die Integrandenfunktion gilt also  f(-t) = - f(t)  in ℝ

→   f  ist punktsymmetrisch zum Ursprung.

Deshalb ist   _-a∫^a   f(t)  dt  =  0 , inbesondere also  auch   _-1∫¹  f(t)  dt  =  0   

weil sich die negativen und positiven Anteile (unter- und oberhalb der t-Achse) ausgleichen:

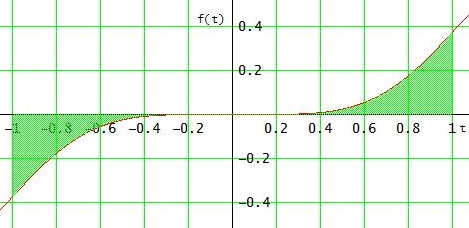
Gruß Wolfgang