geometrische Interpretation einer linearen Abbildung

Question

Ich habe eine Aufgabe, wo ich eine geometrische Interpretation einer linearen Abbildung geben soll? 
Leider habe ich keine Ahnung was von mir gefordert ist bzw. was ich jetzt machen soll. 
Ich habe eine Matrix und als Tipp die Einheitsvektoren? Kann mir vielleicht einer helfen? MfG

Answer 1

Hallo altinstinkt,

mit linearer Abbildung ist wohl eine Abbildung mit der Vorschrift \( f(x) = \begin{pmatrix}-1 & 0\\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix}x \\ y \end{pmatrix} \) gemeint.

Ich nehme also an, Du sollst die Matrix mit den Einheitsvektoren multiplizieren.
Matrix mal dem ersten Einheitsvektor ergibt \( \begin{pmatrix}-1 \\ 0 \end{pmatrix} \).
Matrix mal dem zweiten Einheitsvektor ergibt \( \begin{pmatrix}0 \\ 1 \end{pmatrix}  \).
Hier kann man die Interpretation bereits erahnen. Deutlicher wird es wenn man die Matrix mit einem beliebigen Vektor \( \begin{pmatrix} x \\ y \end{pmatrix} \) multiplizert, das ergibt \( \begin{pmatrix}-x \\ y \end{pmatrix} \).

Wie ist nun die Interpretation? Die Abbildung ändert die Richtung der x-Komponente eines Vektors.

Answer 2

Die Eigenwerte berechnen sich aus

$$(-1 - \lambda)(1- \lambda)=0 \quad \Rightarrow  \space \lambda_1=1; \space \lambda_2=-1$$

Die zugehörigen Eigenvektoren sind dann

$$e_1=\begin{pmatrix} 0 \\ 1\end{pmatrix} \space \text{und} \space e_2=\begin{pmatrix} 1 \\ 0\end{pmatrix}$$

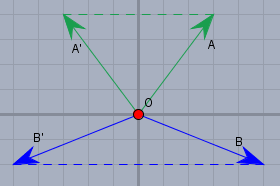
wobei \(e_1\) stets auf sich selbst abgebildet wird und \(e_2\) jeweils negiert wird - geometrisch bedeutet das eine Spiegelung an der Y-Achse. Wie folgendes Bild zeigt

Gruß Werner