Geometrische Interpretation von | 1-x | ≤ c · (1 - |x|)

Question

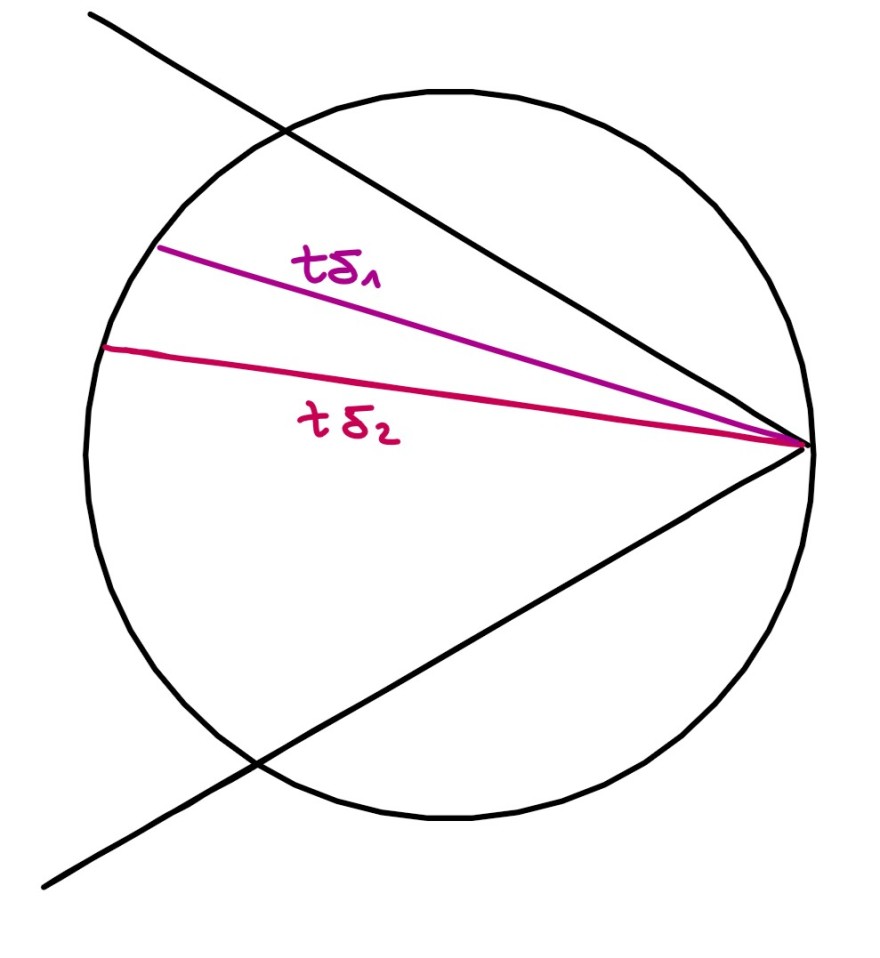
Aufgabe: Graphische Interpretierung von | 1-x | ≤ c · (1 - |x|) für einen Parameter c > 0 und x aus der Komplexen Einheitskreisscheibe.

Problem/Ansatz: Ich verstehe, dass die Ungleichung bedeutet, dass der Abstand von x zur 1 um einen konstanten Faktor kleiner sein muss als der Abstand zum Rand. Mit anderen Worten, man bleibt (außer im Punkt 1) immer ein bisschen vom Rand entfernt. Ich habe mal eine kleine Skizze gemalt... mir ist bewusst, dass die Menge der Punkt, die die Ungleichung erfüllen, links noch vom Rand entfernt sein müsse.

Es fällt mir aber leider sehr schwer diese Menge mir genau vorzustellen, bzw. eine Geometrische Interpretation zu finden. Hat jemand eine Idee?

Comments

Veranschaulichung : a ≤ c·b

Nachweis :

Betrachte x -> -1

Answer 1

HALLO

Umschreiben zu |z-1|+c|z-0|=<c also Abstand zu 1 + c fache Abstand zu 0 =c ist der Rand der Menge

kann man mal für c=1 etwa untersuchen, da ist es die Strecke zwischen 0 und 1

dann mal c=1/2 und c=2 erst die Punkte auf der  Strecke, dann senkrecht dazu

eine eindeutige  geometrische Figur hab ich nicht gesehen

lul

Comments

Ich hatte die Aufgabe falsch verstanden, nämlich dass die Existenz eines (einheitlichen) c, das für alle x aus der komplexen Einheitskreisscheibe die Ungleichung erfüllt, nachgewiesen werden soll, was nicht möglich ist.

Umgekehrt ist aber tatsächlich für festes c>0 die Lösungsmenge der Ungleichung gesucht. Diese Lösungsmenge ist eine Kreisscheibe mit dem durch die beiden Zahlen 1 und (1-c)/(1+c) begrenzten Durchmesser.

---

@ Gast hj2166

Kannst du bitte den Kreis für c=1/2 und c=2 mal hinschreiben?

lul

---

sieht so aus :