Hallo theoretiker,
seien \(a,b,c,d,e,f,g,h,i\in\mathbb{G}\) mit \(\mathbb{G}:=\{0,1,2,...,255\}\) \(9\) Grauwerte, die wie folgt in einem Bild angeordnet sind: $$\begin{matrix}a&b&c\\d&e&f\\g&h&i\end{matrix}$$ Sei weiterhin $$\min{(a,b,c):=\min{(\min{(a,b)}},c)}$$ und $$\min{(a,b)}:=\begin{cases}a & \text{ falls } a\leq b\\b & \text{ sonst } \end{cases}$$
Für den Erosions-Filter kannst Du dann z.B. durch $$\min{(a,b,c,d,e,f,g,h,i)}=\min{(\min{(a,b,c)},\min{(d,e,f)},\min{(g,h,i)})}$$ zeigen, dass sich dieser Filter in einen horizontalen und vertikalen Anteil aufteilen lässt. Der Filter würde dann wie folgt funktionieren: erst wird für jedes Pixel das Minimum aus linkem und rechtem Nachbarn (sowie dem Pixel selbst) gebildet und gespeichert. Auf diesem gebufferten Bild erfolgt dann der gleiche Prozess in vertikaler Richtung. Du erhältst auf diese Weise das selbe Bild wie durch das Betrachten der \(9\times9-\)Matrix.
Für den Median-Filter gilt diese Aufteilung nicht. Wir betrachten dazu folgendes Grauwertbild (keine Randbetrachtung; Änderungen im rot markierten Bereich):
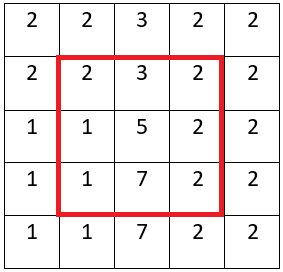
Die Anwendung des nicht separierten Median-Filters ergibt:
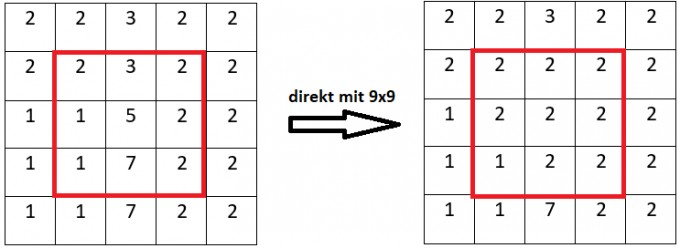
Die separierte Variante liefert:
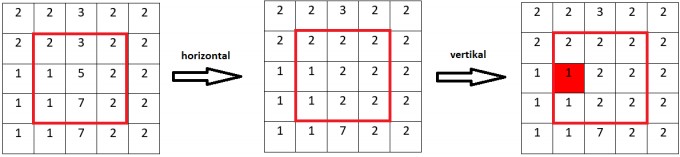
Wie man an dem rot markierten Pixel sieht, sind die Bilder nicht identisch. Man kann durch die Aufteilung zwar auch einen Median-Filter bauen, der aber von der nicht separierten Variante abweichende Ergebnisse liefert. Im Allgemeinen gilt: $$med{(a,b,c,d,e,f,g,h,i)}\neq med{(med{(a,b,c)},med{(d,e,f)},med{(g,h,i)})}$$
Spezialfälle (z.B. homogene Bilder) sind natürlich die Ausnahme. Ich habe übrigens mal ein interessantes Paper gelesen, in dem es um die Konstruktion eines separierbaren Median-Filters zur Reduktion von Bildrauschen ging. Allerdings differieren die Ergebnisse dieses Filters und der Variante, von der ich vermute, dass Du sie in Deiner Frage meinst (https://de.wikipedia.org/wiki/Rangordnungsfilter#Medianfilter). Das Paper findest Du hier: http://ieeexplore.ieee.org/document/4767047/ (erfordert einen Zugang; den solltest Du von der Uni aus haben).
André