Lineare Dgl 2.Ordnung inhomogen.Richtungsfeld zeichnen, spezielle Lösungen bestimmen, Kurven einzeichnen

Question

wie löse ich diese Aufgabe? Siehe Bild.

Comments

EDIT: Wie kommst du hier auf 2. Ordnung in der Überschrift?  https://de.wikipedia.org/wiki/Gew%C3%B6hnliche_Differentialgleichung#Allgemeine_Definition 

---

Auf diese Überschrift komme ich, weil diese Aufgabe bei uns im Skript unter der Rubrik mit dieser Überschrift steht. Genauer Rubrikname: Inhomogene lineare Dgl 2. Ordnung mit konstanten Koeffizienten

---

Die DGL in der Aufgabe hat aber die Ordnung 1 (kein y"). Deshalb die Nachfrage von Lu :-)

---

Ja, das stimmt. Aber mehr als das was ich schrieb, kann ich leider nicht sagen. Da ich keine Idee zur Lösung dieser Aufgabe hatte, habe ich da gar nicht drüber nachgedacht.. Bringt es denn was die Überschrift zu ändern..

Answer 1

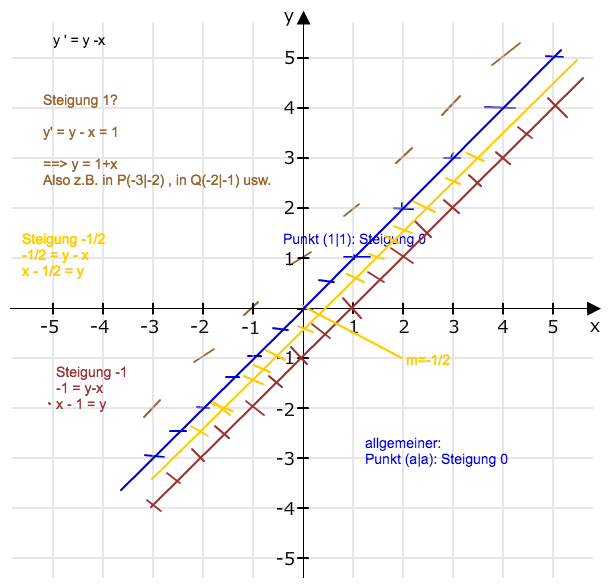
Hier mal ein Anfang für das Richtungsfeld: 

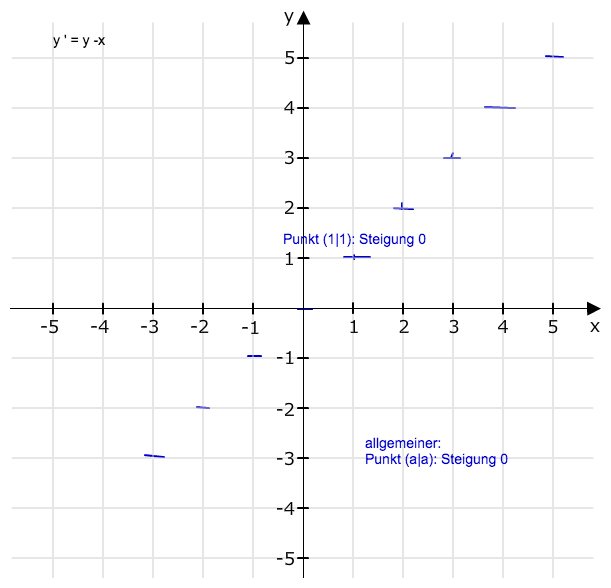
Auf der Geraden y=x ist die Steigung überall 0. 

Ergänze weitere Elemente des Richungsfeldes. Z.B. an Stellen, an denen die Steigung 1 oder 2 oder -1 ... ist. 

Zeichnen kannst du z.B. damit https://www.matheretter.de/rechner/geozeichner . Ein etwas kleinerer Ausschnitt aus dem Koordinatensystem gehört dann in dein Heft. 

Ich habe noch etwas weiter gemacht. 

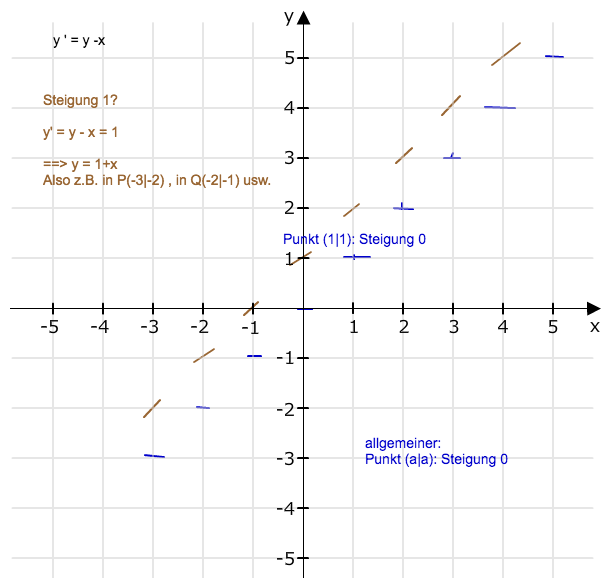
Die Punkte mit y' = 1 können entlang des Richtungsfeldes verbunden werden. Das liefert gerade eine Lösung der Differentialgleichung. Nämlich die Gerade mit der Gleichung y - x = 1, d.h. y = x + 1 . Und diese ist eine Lösung, die die y-Achse in y=1 schneidet. 

Fortsetzung (Kleine Pfeile des Richtungsfeldes sind auf jeder der farbigen Geraden jeweils parallel zueinander):