Extremwertprobleme mit Nebenbedingungen Gesucht a)max. Flächeninhalt und b) max. Umfang

Question

f(x)=-x²+9

Die Punkte A,B,C und D bilden ein Rechteck (in der Parabel)

A(-u / 0) ; B( u / 0); C(u / f(u); D (-u / f(-u) UND 0<u<3

Bitte um ausfühliche Vorgehensweise der Schritte (nicht die Endergebnisse)

Answer 1

Die Angelegenheit ist symmetrisch.
Wir brauchen nur den rechten Teil
berechnen..

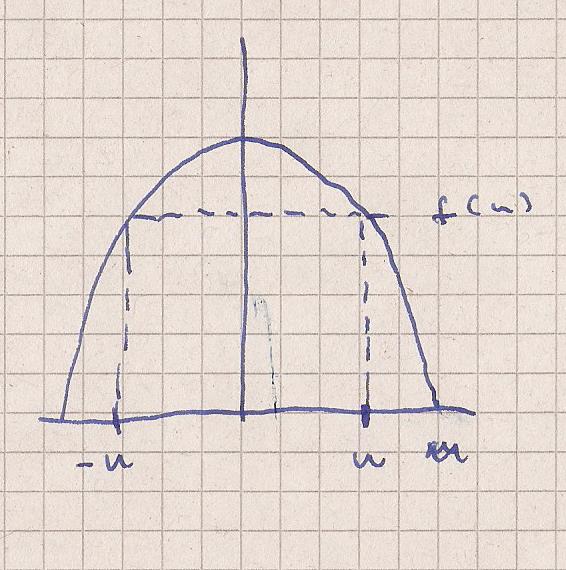
f(x)=-x²+9

a.) Flächeninhalt
( rechter Teil )
A ( u ) = u * f ( u )
A ( u ) = u * ( - u^2 + 9 )
A ( u ) = - u^3 + 9 * u
A ´( u ) = -3* u^2 + 9
Extremwert
-3* u^2 + 9 = 0
u^2 = 3
u = ± √ 3
Den Wert in die Ausgangsfunktion einsetzen
und mal 2 nehmen ( für links und rechts ).

b.) Umfang
rechter Teil
U ( u ) = 2 * u + f ( u )
U ( u ) = 2 * u + ( -u^2 + 9 )
U ( u ) = 2 * u - u^2 + 9
U ´( u ) = 2 - 2 * u
2 -2 * u = 0
u = 1
Den Wert in die Ausgangsfunktion einsetzen
und mal 2 nehmen ( für links und rechts ).

Bei Bedarf nachfragen.