Tan groesser als der Sin eines Winkels

Question

Ist es eigentlich so, dass der tan eines beliebigen Winkels immer grösser als der sin ist?

Kann man das auch am Einheitskreis zeigen?

Answer 1

Der Tangens kann natürlich auch kleiner sein. Siehe folgenden Einheitskreis

Selber mit dem Programm spielen unter

https://www.matheretter.de/mathe-programme?id=110

Answer 2

dass gilt nur betragsmäßig, da beispielsweise tan(-45°)=-1<sin(45°)=-1/√2 .

Es gilt:

$$|cos(\alpha)|<=1\\\frac { 1}{ |cos(\alpha)| }>=1 |*|sin(\alpha)|\\|\frac { sin(\alpha)}{ |cos(\alpha) }|>=|sin(\alpha)|\\|tan(\alpha)|>=|sin(\alpha)|$$

Anschaulich am Einheitskreis:

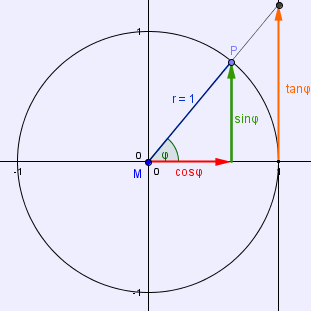
Die beiden Dreiecke sind zueinander ähnlich, aber die Grundseite ist in dem Dreieck mit dem Tangens länger, daher ist die tangens-Seite länger als die Sinus-Seite (ohne Beachtung des Vorzeichens)