Hallo Julian,
das ist eine von diesen Standdard-Optimierungsaufgaben, die jeder einmal bekommt .... schau Dir folgende Skizze an. \(c\) und \(b\) seien die Katheten des Dreiecks:
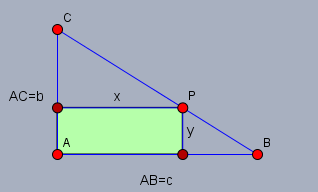
Die Fläche \(F\) des Rechtecks ist \(F=x\cdot y\). Lt. Strahlensatz ist (Strahlzentrum in \(C\))
$$\frac{x}{c} = \frac{b-y}{b} \quad \Rightarrow x=\frac{c(b-y)}{b}$$
Das in die Gleichung für die Fläche einsetzen gibt:
$$F=x \cdot y=\frac{c(b-y)}{b} \cdot y=c\cdot y - \frac{c}{b}y^2$$
Nach \(y\) ableiten und Nullsetzen der Ableitung gibt
$$\frac{\partial F}{\partial y}= c - 2\frac{c}{b} \cdot y \quad \Rightarrow y_{opt}=\frac{b}{2}$$
Einsetzen in die Gleichung für \(x\) gibt \(x_{opt}=c/2\). Falls irgendwas nicht klar sein sollte, so frage bitte nach.