zeichne dir das Dreieck \(ABC\) noch mal extra auf:
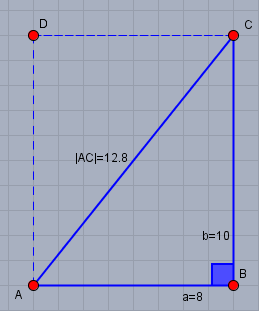
Das Dreieck ist rechtwinklig und demnach besteht nach dem Satz des Pythagoras ein Zusammenhang zwischen den Katheten und der Hypotenuse des Dreiecks. Es gilt (alle Masse in cm)
$$AC^2= a^2 + b^2 \quad \Rightarrow \space AC=\sqrt{a^2+b^2}= \sqrt{8^2+10^2}=\sqrt{64 +100}=\sqrt{164}\approx12,8$$
Als nächstes zeichne Dir das Dreieck \(ACE\) ebenfalls auf
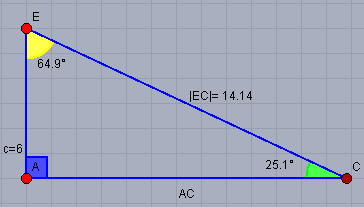
auch hier findest Du ein rechtwinkliges Dreieck. Es gilt
$$EC^2 = AC^2 + c^2 \quad \Rightarrow \space EC=\sqrt{164+6^2}=\sqrt{200} \approx 14,1$$
Den grünen Winkel \(\alpha\) bei \(C\) kann man über den Tangens bestimmen. Es gilt Tangens gleich Gegenkathete zu Ankathete:
$$\tan( \alpha ) = \frac{c}{AC} \quad \Rightarrow \space \alpha = \arctan(\frac{c}{AC}) = \arctan{\frac{6}{12,8}} \approx 25,1°$$ den gelben Winkel \(\beta\) beim Punkt \(E\) bekommt man über die Winkelsumme des Dreiecks
$$\beta = 180° - 90° - 25,1° = 64,9°$$
zu b) Die 8 kongruenten Dreiecke findest Du, indem Du in die Ober- und Unterseite des Quaders jeweils die Flächendiagonale (s. 4 roten Strecken) einzeichnest und auf jede Flächendiagonale kann man zwei Dreiecke 'stellen'.
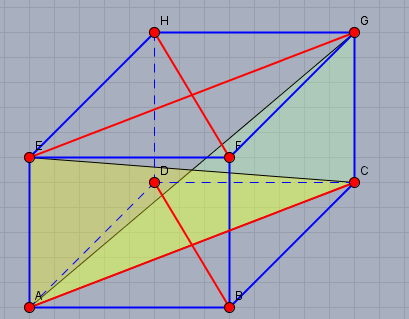
ich habe Dir beispielhaft die beiden Dreiecke auf \(AC\) eingezeichnet.
zu c) den Winkel \(BHE\) (grün) bekommst Du wieder über den Tangens, da der Winkel \(HEB\) beim Punkt \(B\) ein rechter ist.
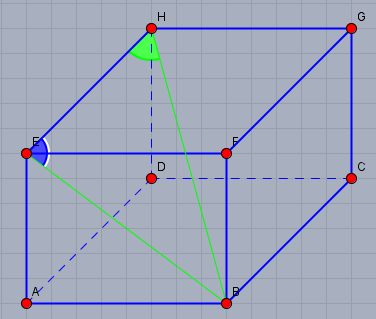
Es gilt
$$\tan(BHE) = \frac{BE}{HE}$$
\(HE=b\) und \(BE=\sqrt{a^2 + c^2}\) also ist
$$BHE = \arctan\left( \frac{\sqrt{a^2 + c^2}}{b} \right) = \arctan\left( \frac{\sqrt{8^2 + 6^2}}{10} \right) = 45° $$
und \(ABH\) überlasse ich Dir - zur Kontrolle: \(ABH\approx 58,0°\)
Gruß Werner