Dein Ergebnis 2,7m3 ist richtig. Für b) bilde die Seiten des Quadrats als Vektoren im Raum ab sowie den Vektor \(v\cdot t \) als dritten Vektor des Spats und berechne dann das Volumen.
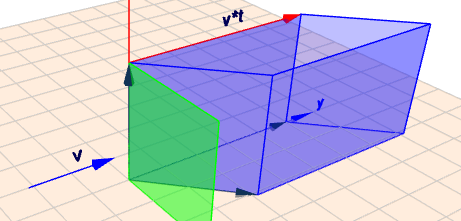
(klick auf das Bild)
(Bem.: ich habe hier die Y-Achse als Richtung für die Geschwindigkeit gewählt - d.h. \(\vec{v} \cdot t=(0; v\cdot t; 0)^T\) ) \(s\) sei die Seitenlänge des Quadrats und \(\varphi\) der Winkel um den es gedreht wurde. Die Seitenvektoren \(a\) und \(b\) des Quadrats sind dann
$$a=\begin{pmatrix} s \cdot \cos \varphi\\ s \cdot \sin \varphi \\ 0 \end{pmatrix}; \quad b=\begin{pmatrix} 0 \\ 0 \\ s \end{pmatrix}$$
Dann ist das Spatprodukt, bzw. das Volumen des Spats
$$V=(a, v\cdot t, b)= (a \times (v \cdot t)) \cdot b = s^2 \cdot v \cdot t \cdot \cos \varphi$$
(Bem.: die Reihenfolge ergibt sich aus dem gewählten Koordinatensystem) Für \(\varphi=0°\) ergibt sich das das obige Ergebnis von \(V(\varphi=0°)=2,7\text{m}^3\) und für \(\varphi=\pi/4\) sind es dann \(V\approx 1,91 \text{m}^3\)