Zeichne Dir ein Weg-Zeit-Diagramm - d.h. eine Graphik, die die Wege von Helmut und Klaus über der Zeit zeigt.
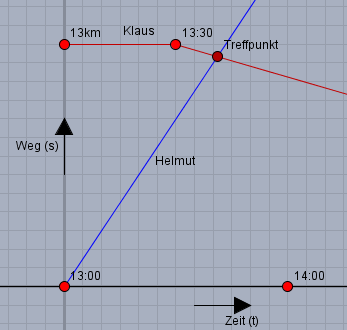
Dort siehst Du die blaue Gerade, die zeigt, wie weit Helmut mit dem Fahrrad kommt , wenn er von Arnheim nach Kirchberg (13km) radelt und die rote geknickte Linie zeigt den Ort von Klaus, der bis 13:30 zu Hause (also in Kirchberg) bleibt und dann auf Helmut zugeht. Beide treffen sich, wenn sie zum selben Zeitpunkt am selben Ort sind, also dort wo sich die blaue mit der roten Linie schneidet.
Man kann nun für beide Wege eine Geradengleichung aufstellen. \(s_H(t)\) ist der Weg von Helmut und \(s_K(t)\) ist der Weg von Klaus nach 13:30. Um 13:00 soll \(t=0\) sein. Es ist
$$s_H(t) = 18 \frac{\text{km}}{\text{h}} \cdot t$$
$$s_K(t) = -3,5 \frac{\text{km}}{\text{h}} (t - 0,5\text{h}) + 13 \text{km}$$
Den Schnittpunkt findet man durch Gleichsetzen beider Gleichungen
$$18 \frac{\text{km}}{\text{h}} \cdot t = -3,5 \frac{\text{km}}{\text{h}} (t - 0,5\text{h}) + 13 \text{km}$$
$$\Rightarrow \space t \approx 0,6860 \text{h} \approx 41,2 \text{min}$$
Die beiden treffen sich also nach gut 42Minuten ca. 650m vor Kirchberg.
Gruß Werner