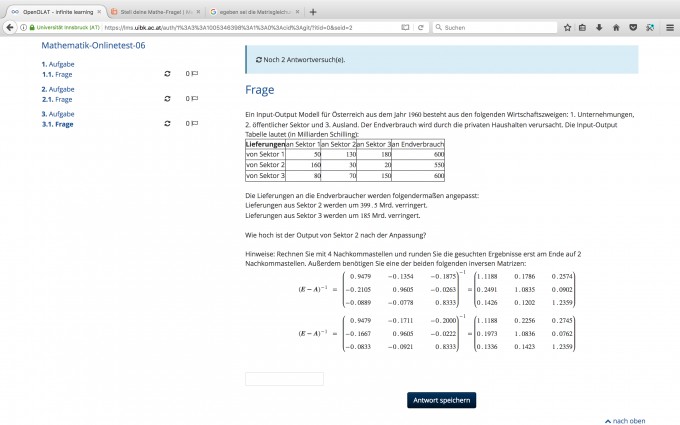
Ein Input-Output Modell für Österreich aus dem Jahr 1960 besteht aus den folgenden Wirtschaftszweigen: 1. Unternehmungen, 2. öffentlicher Sektor und 3. Ausland. Der Endverbrauch wird durch die privaten Haushalten verursacht. Die Input-Output Tabelle lautet (in Milliarden Schilling):
| Lieferungen | an Sektor 1 | an Sektor 2 | an Sektor 3 | an Endverbrauch |
| von Sektor 1 | 50 | 130 | 180 | 600 |
| von Sektor 2 | 160 | 30 | 20 | 550 |
| von Sektor 3 | 80 | 70 | 150 | 600 |
Die Lieferungen an die Endverbraucher werden folgendermaßen angepasst:
Lieferungen aus Sektor 2 werden um 399.5 Mrd. verringert.
Lieferungen aus Sektor 3 werden um 185 Mrd. verringert.
Wie hoch ist der Output von Sektor 2 nach der Anpassung?
Hinweise: Rechnen Sie mit 4 Nachkommastellen und runden Sie die gesuchten Ergebnisse erst am Ende auf 2 Nachkommastellen. Außerdem benötigen Sie eine der beiden folgenden inversen Matrizen:
| (E-A )-1 = ( 0.9479 -0.1354 -0.1875 -0.2105 0.9605 -0.0263 -0.0889 -0.0778 0.8333 )-1 =( 1.1188 0.1786 0.2574 0.2491 1.0835 0.0902 0.1426 0.1202 1.2359 ) (E-A )-1 = ( 0.9479 -0.1711 -0.2000 -0.1667 0.9605 -0.0222 -0.0833 -0.0921 0.8333 )-1 =( 1.1188 0.2256 0.2745 0.1973 1.0836 0.0762 0.1336 0.1423 1.2359 ) |
,
ich sitze gerade bei der Vorbereitung für die nächste Mathe Klausur an folgender Musteraufgabe fest. Leider habe ich keinerlei Ansatz wie ich auf die richtige Lösungsmöglichkeit kommen soll. Kann mir jemand behilflich sein?
Vielen lieben Dank schon vorab.