Gegeben ist die Funktion f mit f (x) = 3/4 x2 -3x
a) Berechnen Sie die mittlere Änderungsrate von f auf dem Intervall I= (2,5)
[ f(5) - f (2 ) ] / ( 5-2 )
m = 2.25
b) Bestimmen Sie die Gleichung der Sekante g durch die Punkte P (2/f (2)) und Q (5/f (5)).
f(5) = m * 5 + b
15/4 = 2.25 * 5 + b
b = -7.5
s ( x ) = 2.25 * x - 7.5
Zeichnen Sie die Schaubilder von f und g in ein Koordinatensystem
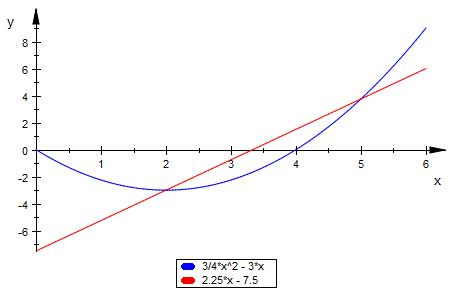
c) Ermitteln Sie momentane Änderungsrate von f an der Stelle x= 2
f (x) = 3/4 x2 -3x
f ´( x ) = 1.5 * x -3
f ´( 2 ) = 1.5 * 2 -3 = 0