Arithmetisches Mittel. Wie kann man Nullfolge b_(n) beweisen? b_(n) := 1/n Summe_(k=0)^n a_(k)

Question

hello es geht hier um Nullfolgen
Meine Frage ist

Arithmetisches Mittel. Wie kann man Nullfolge b_(n) beweisen? b_(n) := 1/n Summe_(k=0)^n a_(k) , n≥1 

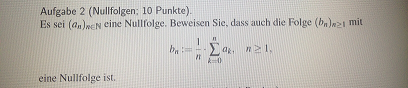
ich weiss die Lösung sollte mit "Cauchyscher Konvergenzsatz" oder mit "(a_1+...+a_n)/n" zu tun haben,jedoch weiss ich leider nicht wie ich anfangen soll

ich hoffe ihr könnt mir helfen

Answer 1

Zu jedem \(\varepsilon>0\) gibt es ein \(N\) mit \(|a_k|<\varepsilon\) für \(k>N\). Splitte die Summe in zwei Teile: $$b_n=\frac{1}{n}\sum_{k=0}^Na_k+\frac{1}{n}\sum_{k=N+1}^na_k$$

Comments

hi :)
also für 1/n hab ich bewiesen warum sie ein Nullfolge ist
sei K > 0
wähle N > 1/ K . (<-> K > 1/N)
für n >= N gilt :
|a_{n} | = |1/n| =1/n =< 1/N < K

aber für die summe leider nicht bzw. weiter komme ich nicht

---

Wenn Dir die Beweisidee alleine nicht reicht, kannst Du den kompletten Beweis des Cauchyschen Grenzwertsatzes bei Heuser (Lehrbuch der Analysis, Teil 1) auf den Seiten 176-177 in aller Ausfuehrlichkeit nachlesen.