Steckbriefaufgabe: Graph von f berührt die x-Achse an der Stelle 4 und hat an der Stelle 8/3 eine Wendestelle.

Question

Bestimme eine ganzrationale Funktion f dritten Grades

für den graph gilt:
 der graph von f berührt die x-achse an der Stelle 4 und hat an der Stelle 8/3 eine Wendestelle. Die Wendetangente hat die Steigung -4/3
danke, schon mal für die hilfe.

Comments

Welchen Grades?

---

dritten grades :)

---

Oben korrigiert :)

Answer 1

der graph von f berührt die x-achse an der Stelle 4

f(4) = 0
f'(4) = 0

und hat an der Stelle 8/3 eine Wendestelle.

f''(8/3) = 0

Die Wendetangente hat die Steigung -4/3

f'(8/3) = -4/3

 

Ich erhalte die Gleichungen:

64·a + 16·b + 4·c + d = 0
48·a + 8·b + c = 0
16·a + 2·b = 0
64/3·a + 16/3·b + c = -4/3

 

Daraus folgt die Lösung bzw. die Funktion

f(x) = 0,25·x^3 - 2·x^2 + 4·x

Comments

Ich komme aber nicht auf das Ergebnis :/

Answer 2

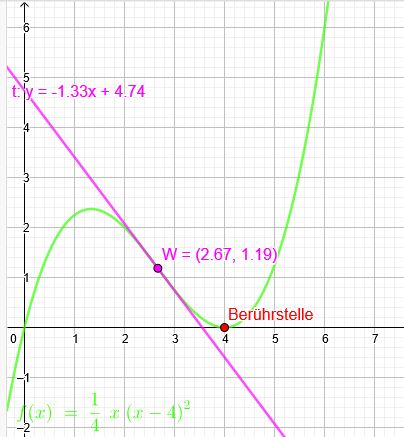
3.Grad  Der Graph von f berührt die x-Achse an der Stelle \(x=4\) und hat an der Stelle \(x=\frac{8}{3} \) eine Wendestelle. Die Wendetangente hat die Steigung \(m=-\frac{4}{3}\)

Doppelte Nullstelle an der Stelle \(x=4\):

\(f(x)=a[(x-4)^2(x-N)]\)

Bei \(x=\frac{8}{3} \) eine Wendestelle.

\(f'(x)=a[(2x-8)(x-N)+(x-4)^2]\)

\(f''(x)=a[2(x-N)+ (2x-8)  + (2x-8)]=a[6x-2N-16]\)

\(f''(\frac{8}{3})=a[16-2N-16]=0\)

\(N=0\)

\(f(x)=a[x(x-4)^2]\)

\(f'(x)=a[(x-4)^2+x(2x-8)]\)

Steigung Wendetangente  \(m=-\frac{4}{3}\)

\(f'(\frac{8}{3})=a[(\frac{8}{3}-4)^2+\frac{8}{3}(\frac{16}{3}-8)]=-\frac{4}{3}\)

\(a=\frac{1}{4}\)

\(f(x)=\frac{1}{4}x(x-4)^2\)