Exponentialfunktion integrieren von 2^-x (x als Exponent)

Question

Weiß jemand wie man das Integriert? Bin am verzweifeln

Comments

Tipp: 

2 = e^ (ln(2)) 

Answer 1

$$ \int2^{-x}dx=\int e^{-ln(2)x}dx=-\frac{1}{ln(2)}e^{-ln(2)x}+C=-\frac{1}{ln(2)}2^{-x}+C $$

Answer 2

 

$$\int 2^{-x}dx\\allg. \int a^xdx=\frac{1}{ln(a)}a^x+c\\⇒\boxed{z=-x}\text{Substitution}\\\frac{dz}{dx}=-1\\ dx=-dz\\⇒-\int 2^zdz\\=-\frac{1}{ln(2)}2^z+c\\=-\frac{1}{ln(2)}2^{}-x+c\\=-\frac{1}{ln(2)}2^{-x}+c$$                                              

Answer 3

Hier meine Aufleitung

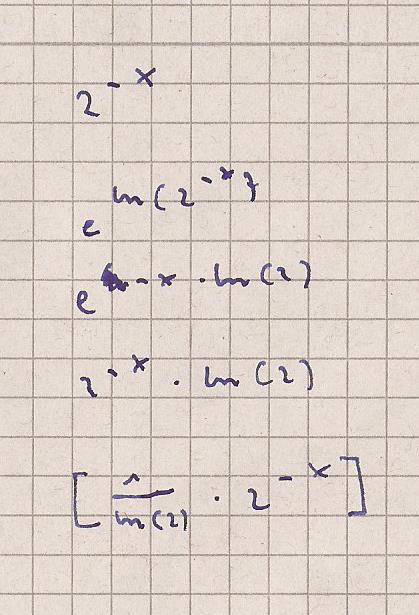
1.Zeile Originalfunktion
2.Zeile : in eine e-Funktion umwandeln
z = e^{ln[z]}
3.Zeile -x vor die Klammer schreiben

Eine e-Funktion kann nur aus einer e-Funktion
kommen. Deshalb probeweise einmal ableiten.
( e^{term } ) ´ = e^term * ( term ´ )

Um auf die Ausgangsfunktion zu kommen
( 1 / ( term ´ ) * e^term ) = e^term
1 / ln(2) * e^{ln[2]*[-x]}
1 / ln(2) * 2^{-x}