Vierecke konstruieren mit 4 angegebene Seiten

Question

Hallo , kann mir bitte jemand erklären wie man diese Aufgaben löst ?

Ich vermute dass man erst mit Seite a anfängt dann den Winkel Alpha =. 70 grad misst aber dann hab ich ein Problem und weiß nicht wie man Rest zeichnet weil das beliebig sein kann und meine Größen dann nicht passen.

Kann mir jemand eine Zeichnung machen ?

Answer 1

Beginne - wie Du schon vorgeschlagen hast - mit der Strecke \(a\), die durch die beiden Punkte \(A\) und \(B\) begrenzt ist. Trage bei \(A\) die \(70°\) ab, und schlage einen Kreis mit \(|d|=8\text{cm}\) um \(A\), der den freien Schenkel des Winkels in \(D\) schneidet.

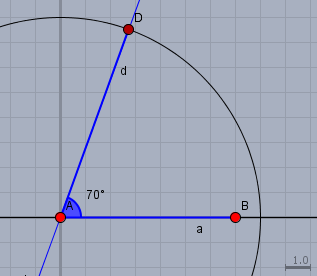
So hast Du schon zwei Seiten und drei Punkte des Vierecks.

i) \(b=6\text{cm}\) und \(c=10\text{cm}\).

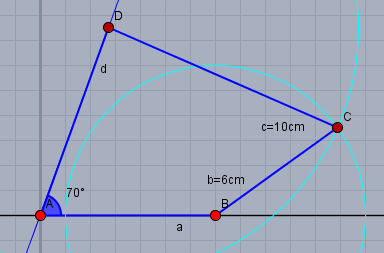
Schlage um \(B\) einen Kreis mit dem Radius \(6\text{cm}\) und um \(D\) einen Kreis mit dem Radius \(10\text{cm}\). Beide Kreise schneiden sich in zwei Punkten - wähle den 'angenehmeren' zu Punkt \(C\).

ii)  \(b=4\text{cm}\) und \(c=6\text{cm}\).

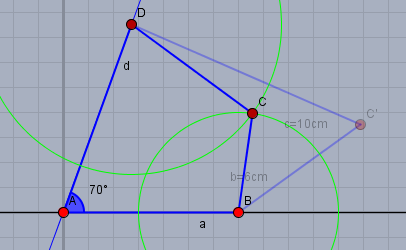
läuft genauso ab. Beide Kreise schneiden sich in einem neuen Punkt \(C\).

iii) \(b=5\text{cm}\) und \(c=3\text{cm}\).

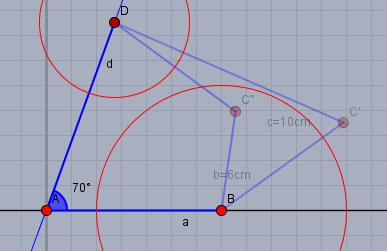
Und hier gibt es keinen Schnittpunkt der beiden Kreise. Also existiert ein solches Viereck nicht.

Gruß Werner

Comments

Tolle Antwort!

---

Danke :-)                    .

---

Eine super Antwort habe alles super verstanden ! Danke für die Mühe.

Eine Frage bleibt offen und zwar woher weiß man um welchen Punkt man mit welchen Radius einen kreis schlagen sollte ? Bei Dreiecken war mir das klar aber 4ecken ist das komplizierter

---

Du fragst: "... um welchen Punkt man mit welchen Radius" interessant! eine Frage, die ich mir selbst nie gestellt habe. Aber im Grunde ist sie berechtigt.

Es wird (implizit) angenommen, dass jedes Viereck - falls nicht anders angegeben - wie folgt aufgebaut ist:

Die Seite \(a\) liegt zwischen den Punkten \(A\) und \(B\), Seite \(b\) zwischen \(B\) und \(C\) usw. Ist ein Punkt \(B\) schon gefunden, und die Länge der Seite \(b\) ist bekannt, so liegt der Punkt \(C\) zwangsläufig auf einem Kreis mit dem Radius \(|b|\) und Mittelpunkt \(B\). Entsprechendes gilt für \(D\) und \(c\). Die Lage von \(D\) ist bekannt und der Punkt \(C\) ist die Länge \(|c|\) von \(D\) entfernt, also liegt \(C\) auf einem Kreis mit Radius \(|c|\) und Mittelpunkt \(D\). Da wo sich die beiden Kreise schneiden sind beide Bedingungen erfüllt.

---

Ich bin dir doch dankbar.

Tut mir leid dass ich ich spät antworte.

Mach weiter so Dankeschön

Answer 2

> dann den Winkel Alpha =. 70 grad misst

Und auf diesem Schenkel liegt im Abstand 8 cm vom Punkt A der Punkt D.

Jetzt einen Kreis um D mit radius 10 cm und einen Kreis um B mit Radius 6  cm.

Schnittpunkt dieser beiden Kreise ist der Punkt C.

> Kann mir jemand eine Zeichnung machen ?

Das würde kaum was helfen. Du sollst die Vierecke konstruieren und nicht zeichnen.