Newtonverfahren wie komme ich auf die Gleichung?

Question

also ich habe die Nulstelle 1,55 (ca.) Ermittelt; doch meine Frage ist, gibt es nur die Nullstelle, oder woher weiß ich, dass es nicht noch mehr Nullstellen gibt? Wie ändert sich meine Funktion f(x)= - x^3 -4x +10  ?? Also damit ich weitere mögliche Nullstellen herausfinde?

Comments

Tipp: \(f^\prime(x)<0\) für alle \(x\).

---

Wie genau ist das gemeint? :S

---

\(f\) ist streng monoton fallend.

---

Heißt das, es gibt keine weiteren Nullstellen? Und das ist aber nicht immer so, oder? Was mache ich bei anderen Funktionen?

---

Eine streng monotone Funktion hat höchstens eine Nullstelle. Eine Methode zur Bestimmung der Anzahl der Nullstellen einer beliebigen Funktion ist mir nicht bekannt.

Answer 1

Hallo Niki,

eine Funktion  f(x) = - x³ + ax + b  ist entweder streng monoton fallend (genau eine Nullstelle) , oder sie sieht wegen der Grenzwerte für x → ± ∞  ungefähr so aus:

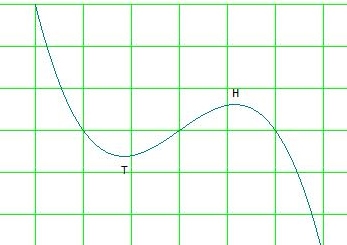
Mit der Ableitung kannst du dann einfach den Hoch-  und den Tiefpunkt ausrechnen. Liegt/liegen

-  beide unterhalb oder beide oberhalb der x-Achse, hast du genau eine Nullstelle

- einer auf der x-Achse, hast du genau zwei Nullstellen

- einer unter- und einer oberhalb der x-Achse, hast du genau drei Nullstellen

Die kannst du dann ggf. mit verschiedenen Startwerten mit dem Newtonverfahrten suchen.

Gruß Wolfgang

Comments

Danke für die Mühe! 

"Die kannst du dann ggf. mit verschiedenen Startwerten mit dem Newtonverfahren suchen."

-> wie macht man das? Hier z.B. in meinem Beispiel kann ich ja  1 oder 2 als Startwert benutzen, heißt das ich muss es für die 1 und dann für die 2 machen? Also dass dann z.B bei dem Startwert 1 der x-Wert 1,55 rauskommt und bei dem Startwert 2 könnte man gucken, ob noch andere Nullstellen vorliegen? Oder wie kann man das verstehen?

---

> ...  könnte man gucken 

Könnte man. Aber hier könnte man ewig suchen und wird keine weiteren Nullstellen finden, weil die Funktion ja streng monoton fallend ist (f'(x) immer negativ) und deshalb keine Extrempunkte hat. 

---

Ahh ok, ich habs jetzt raus, man legt sich ja die Wertetabelle an, und jenachfem wie oft sich die Werte ändern also mag es vom positiven ins negative oder andersrum sein, müsste das der Anzahl der Nullstellen entsprechen. Und wenn ich die gleiche Funktion nur abgeleitet hätte also f'(x) , dann hätte ich durch das Newtonsche Verfahren Extrempunkte raus oder? 

---

Das mit der Wertetabelle ist problematisch, weil sich zwischen zwei ausgewählten Werten das Vorzeichen zweimal ändern könnte, so dass man in der Tabelle die Änderung nicht bemerkt.

---

Wie müsste man dann vorgehen? Stehe aufm Schlauch :-(

---

Im Allgemeinen kommt das auf die Funktion an.

> Stehe aufm Schlauch :-(

Beim Beispiel in  der Frage verstehe ich dein Problem nicht. Das Vorgehen ergibt sich doch aus meiner Antwort.

---

Ich verstehe, wie das zu diesem Beispiel berechnet wird, doch es gibt auch andere Funktionen, die nicht monoton fallend sind bzw. nicht nur 1 Nullstelle haben, sondern mehrere. Ich habe nun gelernt durch die Tabelle, dass eine Nullstelle vorliegt , wenn sich das Vorzeichen ändert. Nur, wenn ich mehrere Nullstellen auszurechnen habe, weiß ich nicht wie ich das anzustellen habe...

---

So allgemein kann man das für "irgendeine Funktion" leider nicht beantworten.