Hallo limonade,
schon aus Gründen der Symmetrie muss für die Seitenlängen des Parallelogramms \(3,5\text{cm}\) heraus kommen. Alle Seiten sind gleich lang.
Mal sehen ob die Rechnung dasselbe ergibt. Schau Dir folgende Zeichnung an:
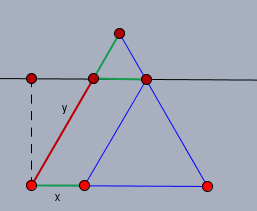
Tipp: wenn Du selber so eine Zeichnung machst, versuche die Strecken (hier \(x\) und \(y\)), die nicht unbedingt im Vorfeld gleich lang sein müssen, auch wirklich unterschiedlich lang in der Skizze zu zeichnen. Dann sieht man besser die Zusammenhänge!
Ist die Grundseite des Parallelogramms \(x\), so findest Du diese Strecke \(x\) an den grün markierten Stellen wieder. Sei die Seite des gleichseitigen Dreiecks \(a\), dann ist \(y=a-x\). Die Höhe \(h\) des Parallelogramms ist
$$h= \frac12 \sqrt{3} \cdot y$$ und die Fläche \(A\) des Parallelogramms ist
$$A = x \cdot h = x \cdot \frac12 \sqrt{3} \cdot y = x \cdot \frac12 \sqrt{3} \cdot (a-x)=\frac12 \sqrt{3} \cdot (ax-x^2)$$ Die Ableitung nach \(x\) ist
$$A'=\frac12 \sqrt{3} (a-2x)$$ und dies ist genau dann \(=0\), wenn \(x=a/2=3,5 \text{cm}\) ist (wie zu erwarten; s.o.).
Gruß Werner