Betrachten Sie ein Rechteck mit Seitenlängen a,b>0 und Umfang 4. Bestimmen Sie a, b so, dass die Fläche maximal ist.

Question

Betrachten Sie ein Rechteck mit Seitenlängen a,b>0 und festem Umfang 4. Bestimmen Sie a, b so, dass die Fläche des Rechtecks maximal ist.

Answer 1

U = 2a + 2b = 4
b = 2 - a

A = a * b
A = a * (2 - a)
A = 2a - a^2

A' = 2 - 2a = 0
a = 1

b = 2 - a = 2 - 1 = 1

a und b müssen 1 sein, damit die Fläche maximal wird. Damit haben wir ein Quadrat.

Comments

Ich weiß nicht, aber ist diese Rechnung nicht vollkommen falsch?
Es muss kein Quadrat errechnet werden, sondern ein Rechteck mit einer maximalen Fläche.

---

Merke: Jedes Quadrat ist ein Rechteck aber nicht jedes Rechteck ist ein Quadrat.

Das Quadrat ist ein besonderes Rechteck.
Es hat von allen Rechtecken mit gleichem Umfang den größten Flächeninhalt.
Es hat auch von allen Rechtecken mit gleicher Fläche, den kleinsten Umfang.

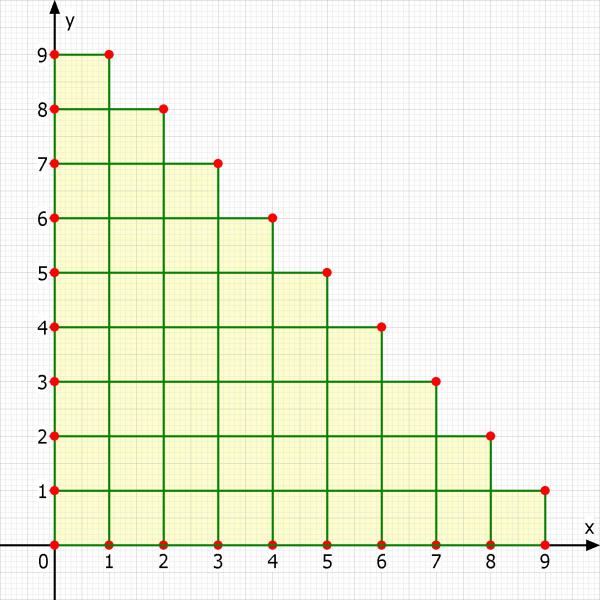
In der folgenden Abbildung habe ich versucht mehrere Rechtecke mit dem Umfang von 20 einzuzeichnen. Dabei liegen alle rechten oberen Ecken der Rechtecke auf einer Geraden. Alle linken unteren Ecken liegen im Koordinatenursprung.

Vielleicht kannst du selber sehen, welches Rechteck die größte Fläche hat. Eventuell hilft nachrechnen.