Hallo limonade,
> b) Auf welcher Kurve liegen alle Wendepunkte der Schar?
Da die Ortskuve die Form y = f(x) haben soll, musst du den die Wendepunkte der Schar bestimmen und aus dem x- und dem y-Wert a eliminieren:
fa(x) = 1/4 * (x4 - a2x)
fa'(x) = x3 - a/2 * x
für a > 0 ergibt (sonst keine Wendepunkte!)
fa"(x) = 3x2 - a/2 = 0 die Wendestellen x1,2 = ± √a / √6
Einsetzen in fa ergibt dann die Wendepunkte W1,2 ( ± √a / √6 | - 5·a2 /144 )
Die Koordinaten (x|y) der Wendepunkte sind also
y = - 5·a2 /144 und x = ± √a / √6 → a = 6x2
a in den y-Term eingesetzt ergibt
y = - 5 · (6x2)2 /144 = - 5/4 x^2
Das ist die Ortskurve, auf der alle Wendepunkte der Kurvenschar liegen.
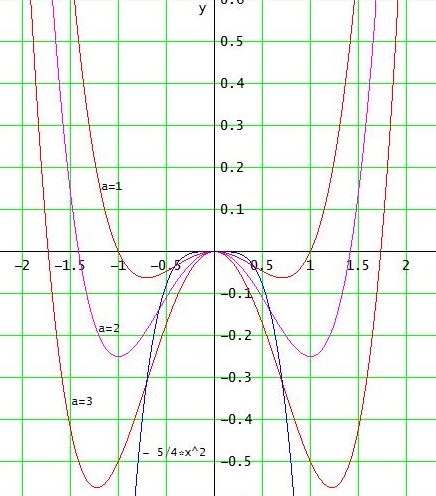
Graphen von f1 , f2 und f3 und der Ortskurve y = -5/4 x2
Gruß Wolfgang