Zeigen sie, (Zn,⊕n,⊙n) ist ein Körper genau dann, wenn n eine Primzahl ist.

Question

Sei n ∈ IN. Zeigen sie, (Z_n,⊕_n,⊙_n) (die ganzen Zahlen mit Addition und Multiplikation modulo n) ist ein Körper genau dann, wenn n eine Primzahl ist.

Answer 1

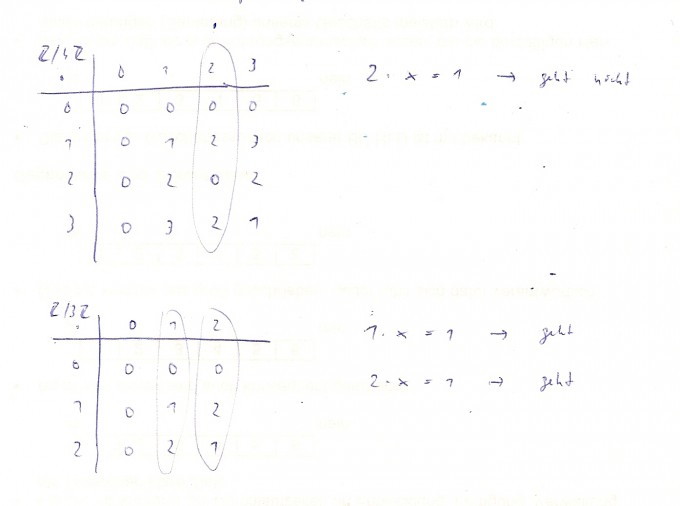
Hallo morrohype, ich habe mal Z/4Z und Z/3Z auf invertierbare bzw. nicht invertierbare Elemente untersucht.  Siehe Bild.  Für a Element Z ist [a] genau dann invertierbar, wenn es ein [b] gibt mit [a] * [b] = [1] ⇔ (a * kn) (b + ln) = 1 + mn ⇔ a * b + q * n = 1.  (I)

Aus dieser Gleichung liest der gewiefte Mathematiker (der ich leider nicht bin) ab:  ggT(a, n) = 1.  (a ungleich 0)

Wenn ggT(a, n) ungleich 1 ist, z. B. n = 4, a = 2, siehe Bild, funktioniert Gl. (I) nicht, und a ist nicht invertierbar.

Das heißt:  n Primzahl ⇔ alle a invertierbar ⇔ Z/nZ ist Körper.