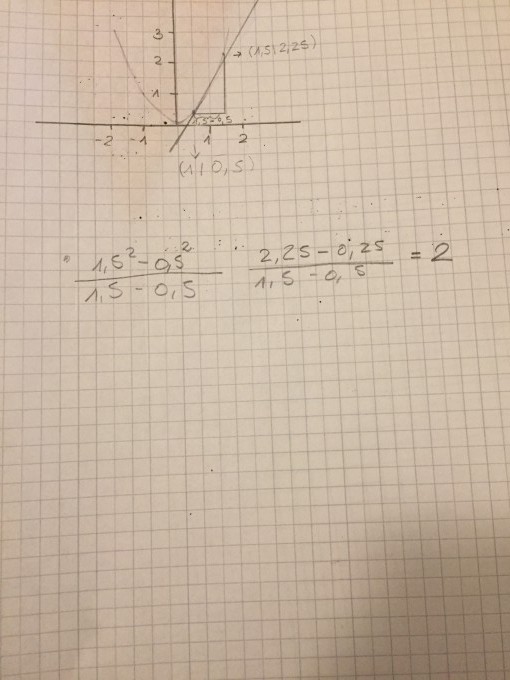Ableitung der quadratischen Funktion y = x^2

Question

Hallo :)

Zwar verstehe ich was die Quadratische Ableitung ist, aber nicht die Aufgabenstellung.

-> a) gib die Ableitung der Quadratfunktion an der Stelle 3 und -4 an

b) An welcher Stelle hat die Quadratfunktion die Ableitung 8 und -6 ?

Habe bereits eine Aufgabe zur Quadratischen Funktion gemacht, wäre es so richtig/ muss ich auch so vorgehen um die Aufgaben zu berechnen? (Foto)

Wäre super, wenn mir jemand helfen kann!!

Comments

Habt ihr bereits Ableitungen berechnet oder habt ihr bisher die Steigung nur näherungsweise mit

dem Steigungsdreieck berechnet?

---

Ja, aber nur einmal und das auch mithilfe des Steigungsdreiecks

---

Du kennst doch sicher die Lösungsformel für quadratische Gleichungen. Man kann dort auch etwas machen, indem man die Diskriminante Null setzt. Das ist allerdings ziemlich umständlich. Sobald du die Ableitungen ausrechnen kannst, wird es dann einfacher. 

Answer 1

f(x) = x^2 --> f '(x) = 2x

f '(3) = 6

f '(-4)= -8

b)

f '(x)= 8

2x=8

x= 4

f '(x) = -6

2x=-6

x= -3

Comments

Also einfach die Zahl, zB. 3, mal 2 nehmen? Und bei b) das Gegenteil 

---

Ja, das läßt sich sogar beweisen, dass das bei der 

Quadratfunktion immer   2*x ist.

Answer 2

-> a) gib die Ableitung der Quadratfunktion an der Stelle 3 und -4 an

(3^2 - (3+h)^2 ) /h  = (9-(9+6h+h^2) ) / h  = ( 6h-h^2 ) / h = ( 6-h) / h

und das hat für h gegen 0 den Grenzwert 6, also hat die 

Quadratfunktion an der Stelle 3 den Wert 6

ebenso erhältst du bei -4 den Wert -8

b) An welcher Stelle hat die Quadratfunktion die Ableitung 8 und -6 ?

bei 4 und bei -3 .

Answer 3

Da du eh 4 Aufgaben zu lösen hast empfiehlt
es sich die 1.Ableitung über den Differentialquotienten
nach der delta h Methode zu bestimmen

Die erste Ableitung ist die Funktion der Steigung einer
Funktion
f ( x ) = x^2
f ´ ( x ) = 2x

Aufgaben
a) gib die Ableitung der Quadratfunktion an der
Stelle 3 und -4 an

f ´ ( 3 ) = ?
f ´( -4 ) = ?

b) An welcher Stelle hat die Quadratfunktion die
Ableitung 8 und -6 ?
f ´( x ) = 8
f ´( x ) = - 6

Willst du es jetzt weiter versuchen ?
Gebe Auskünfte bis alle Klarheiten beseitigt sind.

Comments

Wer alle Klarheiten beseitigt, wird am Ende selber beseitigt. 

(Chines. Sprichwort)

Pass also gut auf dich auf! :))

Gluß von Mann aus China mit Staatsbülgelschaft deutschel !

---

Wer alle Klarheiten beseitigt, wird am Ende selber beseitigt.
(Chines. Sprichwort)

Ich bezweifele das dies ein chinesisches
Sprichwort ist. Dann müßte es lauten

Wel alle Klalheiten beseitigt, wild am Ende selbel
beseitigt.

( Kung-fu-tse Vers 123, Absatz 321 )

Befindest du dich gerade in einem Gravitationsfeld oder in einem Aufzug ?

---

In einem Aufzug in einem Gravitationsfeld, das von einem schwarzen Loch erzeugt wird. :)

---

Wir hatten bisher noch nicht die h- Schreibweise, deshalb verstehe ich deine Antwort nicht ganz :D

Muss ich nicht einfach die 3 bzw. -4 mal 2 nehmen? 

Danke

---

Ich hoffe du bist noch nicht zu sehr in die
Länge gezogen worden der Aufzug bewegt sich
nach oben.
Andernfalls sehe ich schwarz für dich.

---

Ja.
f ´ ( x ) = 2x
f ´ ( 3 ) = 2*3 = 6
f ´( -4 ) = 2*(-4) = -8

f ´( x ) = 8 = 2 * x  => x = 4
f ´( x ) = - 6  = 2 * x  => x = -3

---

Okay! Ist das Prinzpi dann gleich, wenn ich die Funktion f(x) = x^2 gegeben habe und 1) f'(5) angeben muss und 2) abweichen Stellen x gilt: f'(x) = 3

---

Deine Fragen verstehe ich nun wiederum nicht.
Aber das macht nichts.
Das kriegen wir geklärt.

Du hast doch schon eine Berechnung mit einem
Steigungsdreieck durchgeführt für

( 1.5 | 1.5 ^2 )
( 0.5 | 0.5 ^2 )

Jetzt die allgemeine Berechnung
( x + h | ( x + h ) ^2 )
( x | x^2 )

( x^2 + 2hx + h^2 - x^2 ) / ( x + h - x )
( 2hx + h^2 ) / h
h * ( 2x + h ) / h
2x + h
Das ist der Differenzenquotient.
Jetzt lassen wird h klitzeklein werden.
lim h −> 0 [ 2x + h ] = 2x
f ´( x ) = 2x

mfg Georg

Ich schaue allerdings jetzt erst einmal
fernsehen.

---

Okay :D

Trotzdem danke :)

---

Hast du meine Antwort verstanden ?
Ansonsten gibt es im Internet auch Lernvideos
Schlagworte

video Mathematik Differenzenquotient
Differentialquotient

Viel Glück.