Finden Sie jeweils ein N ∈ N, so dass |a_n| ≤ 10^{−2} bzw. |a_n| ≤ 10^{−6} für alle n ≥ N ist.

Question

hier ist die Aufgabe:

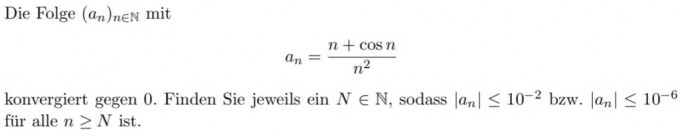
Ich habe soweit folgendes:

\(| \frac{n+cos n}{n^2}| \leq10^{-2} <=> \lim_{n \to \infty}| \frac{n+1}{n^2}| \leq10^{-2} \Rightarrow (*_1)\frac{n+1}{n^2} \leq \frac{2n}{n^2} = (*_3) \frac{2}{n} \Rightarrow (*_2) \frac{2}{n} < 10^{-2}\)

aus der letzen ungleichung folgt:

N_1 ≥ 201

N_2 ≥ 2.000.001

So nun die Fragen... 

wieso verschwinden die Betragsstriche bei \(*_1\)? sollte man da nicht erst (...)² nehmen damit die Wurzel vom Betrag verschwindet und danach alles (..)² machen? .. dann kommt aber ganz was anderes raus...

wieso ist hier bei \(*_2\) ein " < " statt " ≤ "? es ja ja mit der Majorante, die wir finden zutun, also bei \(*_3\). Aber ich weiß nicht wie genau... 

mfg

Comments

*es HAT ja mit der majorante, die... :D

---

Ich habe soweit folgendes: [Formelzeile]

Das ist abstruser Mist mit einer falschen Aequivalenz und deplatzierten Folgepfeilen, was du da getippt hast. Aufzuschreiben ist das als Ungleichungskette: $$\left|\frac{n+\cos n}{n^2}\right|\le\frac{n+1}{n^2}\le\frac{2n}{n^2}=\frac{2}{n}\stackrel{\text{!}}{\le}10^{-2}$$

Answer 1

So nun die Fragen... 

wieso verschwinden die Betragsstriche bei ∗1∗1?

Der Term (n+1) / n^2  ist nie negativ, also können die |...| wegfallen.


wieso ist hier bei ∗2∗2 ein " < " statt " ≤ "?

Wenn es für < gilt, dann jedenfalls auch für ≤

Comments

Wenn es für < gilt, dann jedenfalls auch für ≤

echt? nicht andersrum? du meinst das bestimmt bezogen auf diese Aufgabe, also bräuchte ich mehr Details :D

ne zweite Frage ist, wieso 200 bzw. 201 für 10^-2 stimmt... wenn ich das in \(\left| \frac{n+\cos(n)}{n^2} \right|\)einsetze kommt dchwachsinn raus... ich verstehe das nicht...

mfg

---

Wenn es für < gilt, dann jedenfalls auch für ≤


echt? Ja, denn wenn a<b ist, dann gilt auch a<b oder a=b ;

denn "oder" ist ja schon wahr, wenn einer der Teile wahr ist.

(200 + cos(200)) / 200^2 = 200,49 / 40000 = 0,005..  < 0,01 = 10^{-2}  .

---

ah ok jetzt machts sinn.

vielen dank!