Bilde die Folge der Partialsummen:
| y1 | 0 | 0 |
| y2 | 0,022 | 0,022 |
| y3 | 0,095 | 0,117 |
| y4 | 0,171 | 0,288 |
| y5 | 0,245 | 0,533 |
| y6 | 0,467 | 1 |
In der rechten Spalten stehen die Partialsummen \(s_i\). Die Endesumme ist 1, also sind die Zahlen bereits normiert. Dann eine Graphik zur Veranschaulichung. Die blaue Kurve ist die Lorenzkurve.
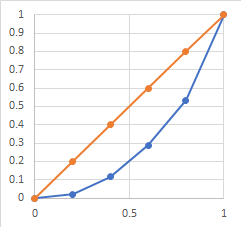
Der Gini-Koeffizient ist nun das Verhältnis der Fläche zwischen der Lorenzkurve (aus den gegeben Zahlen) und der ideallinie für die Gleichverteilung (orange) zu der Fläche unter der Gleichverteilung. Letztere ist im Fall der normieren Darstellung =0,5. Die Fläche \(F_L\) unter der Lorenzkurve ist hier (Summe der Trapezflächen):
$$F_L = \frac12\left(2\sum_{i=1}^6 s_i - s_0 - s_6 \right) \cdot 0,2 = 0,292$$
und dann ist der Gini-Koeffizent \(G\)
$$G= \frac{0,5 - 0,292}{0,5} = 0,416$$