Exponentialfunktion: Kleine Population der Fruchtfliege Drosophila

Question

Im Labor wurde eine kleine Population der Fruchtfliege Drosophila angelegt, deren Bestand angenähert durch N(t) = 40t^2 *e^{1-0,4t} beschrieben wird ( t in Tagen t>0)

a) Bestimmen Sie für die Bestandsfunktion die Nullstellen, Extrema und Wendepunkte

Zeichnen sie den Graphen für 0<t<20

b) Zu welchem Zeitpunkt ist die Population am stärksten ? Wie groß ist die dann ?

c) Zu welchem Zeitpunkt wächst bzw. verringert sich der Bestand besonders stark ?

Ich komme seit Stunden nicht weiter. Hilfe

Answer 1

Hallo Max,

N(t) = 40t² · e^1-0,4·t      ( t in Tagen,  t>0 )

die einzige Nullstelle ist t = 0

a)

mit Hilfe der Produktregel [ u*v ]' = u' * v + u * v'    und  [ e^u ]' = u' * e^u  kannst du die Ableitungen bestimmen:

f '(x) =  16t · (5 - t) · e^{1- 2·t/5)} 

f "(x) =  16/5 · e^{1 - 2·t/5} · (2·t² - 20·t + 25)

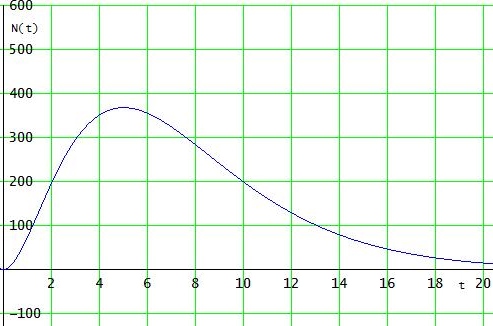
f '(x) = 0   ⇔   t = 5    mit VZW von + → -    →  H(5 | 368)     [ f(5) ≈ 368 ]  

f "(x) = 0  ⇔  2·t² - 20·t + 25 = 0   →   t₁ ≈ 1,46  ;    t₂ ≈ 8.54   jeweils mit VZW

     mit f(1,46) ≈ 130  →   W₁ ( 1,46 | 130 )

      mit f(8,54) ≈ 260  →  W₂ ( 8,54 | 260 ) 

lim_t→∞ f(t) = 0

b)

Wegen  lim_t→0  f(t) = 0 und  lim_t→∞ f(t) = 0   

ist die Population nach 5 Tagen im Hochpunkt am stärksten. 

c) 

Die Bestandsveränderungen sind in den Wendepunkten am stärksten.

Gruß Wolfgang

Comments

zu b)

Die Antwort könnte also lauten:

Die Population ist nach 5 Tagen am stärksten und hat dort etwa 368 Fruchtfliegen.

Ist das richtig?

---

Das ist richtig #######

---

Super, danke für die Rückmeldung :)