Fläche eines eiförmigen Profils berechnen

Question

Hallo Community,

diese Aufgabe wurde  2016 schon mal erklärt ...allerdings verstehe ich die Auflösung nicht so ganz.

Hier die Aufgabe:

Die Flächenformel des Eiprofils (siehe Bild) soll ermittelt werden.

Zur Überprüfung, ob die Formel stimmt, sieht man unter der Zeichnung, dass bei r=1 die Fläche 4,594 groß sein sollte.

Nun bei dem oberen Teil der Fläche handelt es sich wohl um einen  Halbkreis;

bei dem unteren Teil dürfte es sich um 1/4 Kreisfläche handeln - also

r/2 ² * 3,14*1/4

Die Berechnung des Mittelteils erschließt sich mir allerdings nicht so ganz!!

2·pi·(3·r)2 · ATAN(3/4)/(2·pi) ist wohl der Formelteil für den Kreisausschnitt mit dem Radius 3r und dem Winkel Atan 3/4.

Aber was berechnet man mit dieser Formel :

A3 = pi·(r/2)2·(pi - 2·ATAN(3/4))/(2·pi)

Zur Überprüfung, ob die Formel stimmt, sieht man unter der Zeichnung, dass bei r=1 die Fläche 4,594 groß sein sollte.

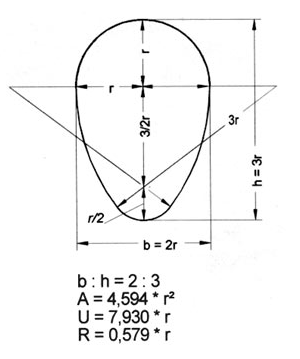
Die Lösung: A1 = 1/2 * pi * r2

                    TAN(α) = (3/2)/2 --> α = ATAN(3/4)

                    A2 = 2·pi·(3·r)2 · ATAN(3/4)/(2·pi) - 2·r·3/2·r

                    A3 = pi·(r/2)2·(pi - 2·ATAN(3/4))/(2·pi)

                   A = 1/2 * pi * r2 + 2·pi·(3·r)2 · ATAN(3/4)/(2·pi) - 2·r·3/2·r +                                           pi·(r/2)2·(pi - 2·ATAN(3/4))/(2·pi)

Vereinfachen und Zusammenfassen ergibt:

A = 4.594130110·r2

Vielleicht kann mir jemand mit Geduld diese Lösung auf Dummie Niveau erklären.

und ein Frohes Osterfest

Klahu65

Comments

Gib einmal den Link von 2016 an.

Der untere Teil mutet wie eine Ellipse an.

Answer 1

Hallo Klahu,

A₁ = Halbkreis

$$ = \frac{1}{2}πr^2 $$

Die Fläche des mittleren Stücks ist der Kreissektor DMG (grün) mit dem Radius 3r abzüglich des Dreiecks ECM.

Zur Berechnung des Sektors wird der Winkel Alpha benötigt.

$$ α=atan \frac{1,5r}{2r}=atan \frac{3}{4} $$

Flächeninhalt eines Kreissektors:

$$ A=π \cdot r^2 \cdot \frac{α}{360} $$

Hier also

$$ A=π \cdot (3r)^2 \cdot \frac{atan \frac{3}{4}}{360} $$

Davon muss der Flächeninhalt des Dreiecks BCM abgezogen werden:

Flächeninhalt Dreieck

$$ A=\frac{2r \cdot 1,5r}{2}=\frac{3}{2}r^2 $$

Jetzt alles noch mit 2 multipliziert, da wir diese Teilfläche zweimal haben:

$$ A_2=2 \cdot(π \cdot (3r)^2 \cdot \frac{atan \frac{3}{4}}{360}-\frac{3}{2}r^2) $$

Das letzte Teilstück lässt sich als ein Kreissektor mit dem Winkel Beta = 2 * (180 - 90 - atan 3/4) = 106,23° und dem Radius 0,5r berechnen:

$$A_3=π \cdot (0,5r)^2 \cdot \frac{106,26}{360} $$

So, ich hoffe, ich habe mich jetzt nirgends vertippt und du verstehst meine Ausführungen.

Comments

Vielen, vielen Dank die Nebelwand hat sich aufgelöst.. :-)

Ich wünsch Dir und allen Teilnehmern hier ein frohes Osterfest.

LG

Klahu65