Wie viele Dreiecke an einen Kreis mit dem Radius 6 cm anlegen?

Question

Heyho, wäre super, wenn sich jemand meiner Problemaufgabe widmen könnte. Ich finde so gar keine Ansatz dafür. Vielen lieben Dank!

Kreisscheibe mit dem Radius 6 cm ... gleichseitige Dreiecke mit Seitenlänge 6 cm ...  [urheberrechtlich geschützten Text entfernt]

 

Ich soll bestimmen, wie viele Dreiecke an den Kreis gelegt werden können, ohne dass sie sich überdecken.

Comments

Matheolympiade :(.

Answer 1

 

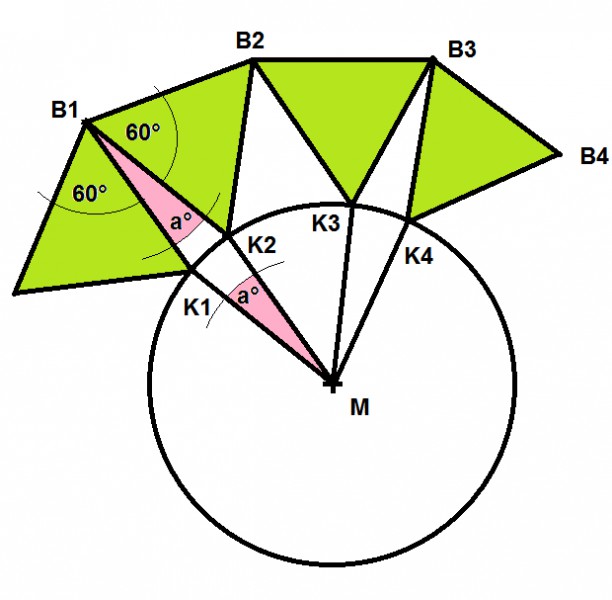
Man überlege sich, dass die Größe des Innenwinkels am Berührpunkt B₁ zweier benachbarter Dreiecksaußenseiten gleich 2 * 60 ° (Innenwinkel eines gleichseitigen Dreiecks ist 60 °, zwei solche Dreiecke berühren sich in B₁) zzgl. dem Winkel zwischen dem Mittelpunkt des Kreises und den beiden Berührpunkten K₁ und K₂ der beiden Dreiecke mit dem Kreis betragen muss.

Denn da der Radius des Kreises gleich der Seitenlänge der Dreiecke ist, ist das Viereck B₁, K₁, M, K₂ ein Parallelogramm (sogar ein Rhombus) und in einem solchen gilt, dass gegenüberliegende Winkel gleich groß sind. Der Winkel K₁B₁K₂ ist also genauso groß wie der Winkel K₁MK₂.

Wenn auf diese Weise ein korrektes, den Kreis ohne Überlappungen vollständig umgebendes n-Eck aus den Dreiecksaußenseiten entsteht, muss dieses n-Eck also eine Innenwinkelsumme W von n * 120 ° zzgl. der Summe aller Winkel K_iMK_i+1 haben. Diese Summe aber ist 360°, denn der Kreis wird durch diese Winkel ja vollständig aufgeteilt.

Somit gilt für die Innenwinkelsumme W des vollständigen n-Ecks:

W = n * 120 ° + 360 °.

Diese Innenwinkelsumme aber muss sich auch mit der Formel für die Innenwinkelsumme eines n-Ecks berechnen lassen, die da lautet: 

W = ( n - 2 ) * 180 °

Es muss also gelten:

n * 120 ° + 360 ° = ( n - 2 ) * 180 °

<=> n * 120 ° + 360 ° = n * 180 ° - 360 °

<=> 720 ° = n * 60 °

<=> n = 12

Das einzige n-Eck, das Inge auf die beschriebene Weise an den Kreis anlegen kann, ist also ein Zwölfeck.