Integralrechnung Einführung

Question

Die Funktion zu den abgebildeten Graphen sind jeweils stückweise über einem Intervall definiert

A) bestimmen Sie jeweils den Flächeninhalt der gefärbten Fläche und das dazugehörige Integral

b) Bestimmen Sie jeweils den Wert des Integrals Integral von -1 bis 1 f(x) dx

Comments

Der Flächeninhalt lässt sich hier leicht mit den Formeln für Dreiecke und Vierecke ermitteln.

Answer 1

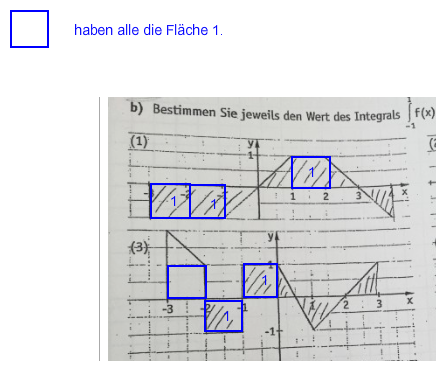
Flächen bestimmen (geometrisch). Zuerst Quadrate, dann Dreiecke:

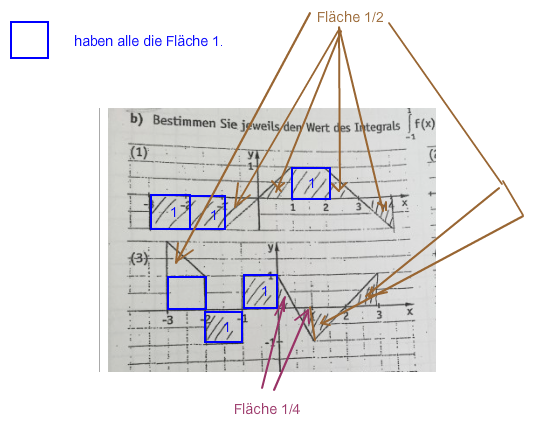
Nun noch die einzelnen Flächen anschreiben:

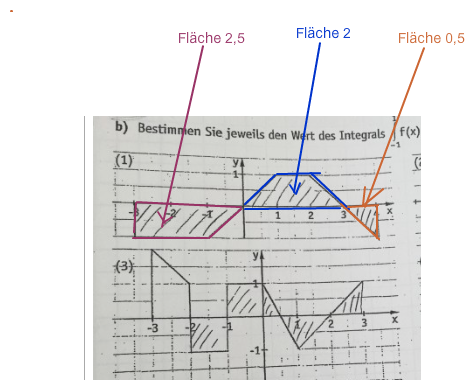
Das dürfte für A) (1) genügen.

Du hast aber leider den Text abgeschnitten. Wenn "der gefärbten Fläche" steht, musst du nun diese Zahlen noch zusammenzählen. 2,5 + 2 + 0.5 = 5.

Das Integral bei A)(1)  ist aber -2,5 + 2 - 0.5 = -1

Beachte, dass bei (3) der Bereich zwischen -3 und -2 nicht (?) eingefärbt ist. Den sollst du dann nicht mit in die Rechnungun nehmen.

Comments

Wieso ist das Integral -1 und nicht 5 ?

---

A)(1) Bei der Integration von -3 bis 4, werden Flächenstücke unter der x-Achse negativ gezählt. Daher meine Rechnung oben:

Das Integral bei A)(1)  ist aber -2,5 + 2 - 0.5 = -1

Answer 2

a) Alle Flächen lassen sich mit elemenarer Geometrie (Flächenformeln) bestimmen. b) Für die Integrale muss man berücksichtigen, dass unterhalb der x-Achse negative Anteile liegen.(1) ergibt 0; (2) ergibt ebenfalls 0; (3) ergibt 1.