z(x) = a·e^{- b·x^2} + c
z'(x) = - 2·a·b·x·e^{- b·x^2}
z''(x) = 2·a·b·e^{- b·x^2}·(2·b·x^2 - 1)
Bedingungen
f(2) = 0
a·e^{- 4·b} + c = 0
f'(2) = -2
- 4·a·b·e^{- 4·b} = -2
f''(2) = 0
a·b·e^{- 4·b}·(16·b - 2) = 0
Aus der letzten Gleichung ergibt sich
16·b - 2 = 0
b = 1/8
Damit lautet die zweite Gleichung
- a/(2·√e) = -2
a = 4·√e
Damit lautet die erste Gleichung
4·√e/√e + c = 0
c = -4
Damit lautet die Funktion
z(x) = (4·√e)·e^{- 1/8·x^2} - 4
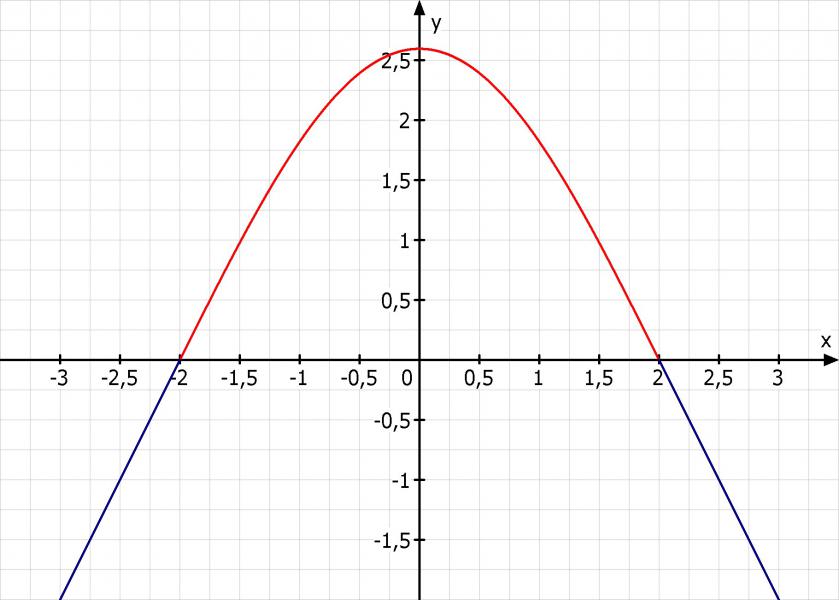
Skizze: