Flächeninhalt Trapez und Raute mit Kreuzprodukt

Question

Wie lautet die Formel für die Berechnung der Fläche einer Raute und eines Trapezes? Ich habe die Formel vorliegen, weiß jedoch nicht was ich mir unter dem Vektoren beim Trapez vorstellen soll. Und bei den Rauten muss man die Länge der Diagonalen multiplizieren und anschließend durch 2 dividieren?

\( A_{\text {Parallelogramm (Raute) }}=|\overrightarrow{A B} \times \overrightarrow{A D}| \)

\( A_{\text {Dreieck }}=\frac{1}{2}|\overrightarrow{A B} \times \overrightarrow{A C}| \)

\( A_{\text {Trapez }}=\frac{1}{2}|(\overrightarrow{A B}+\overrightarrow{D C}) \times \overrightarrow{A D}| \)

Beschriftung Trapez?

\( A_{\text {Raute }}=\frac{1}{2}|\overrightarrow{A C}| \cdot|\overrightarrow{B D}| \)

Diagonalen? Skalarprodukt?

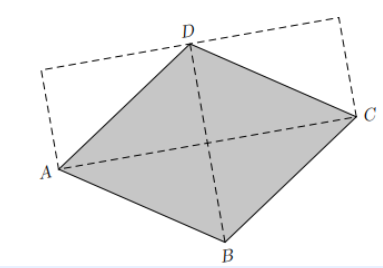
Dankeschön!

Answer 1

Du hast dabei die Punkte A, B, C und D als Ortsvektoren vorliegen.

Der Richtungsvektor AB ergibt sich dann aus dem Ortsvektor B minus dem Ortsvektor A.

AB = B - A

Ja. Rauten kann man über das Produkt der Längen der Diagonalen durch 2 ermitteln. Du kannst aber auch die Formel für das Parallelogramm nehmen. Das Kreuzprodukt ist zwar etwas aufwendiger, spielt aber fast keine Rolle denke ich.