Analysis: Sinus- und Cosinus Funktionen

Question

Ich habe hier eine Aufgabe wo ich ungefähr weiß wie ich vorgehen muss. Also ich weiß, dass ich die beiden Funktionen gleichsetzen muss, aber ich komm wegen dem Sinus und cosinus nicht weiter:

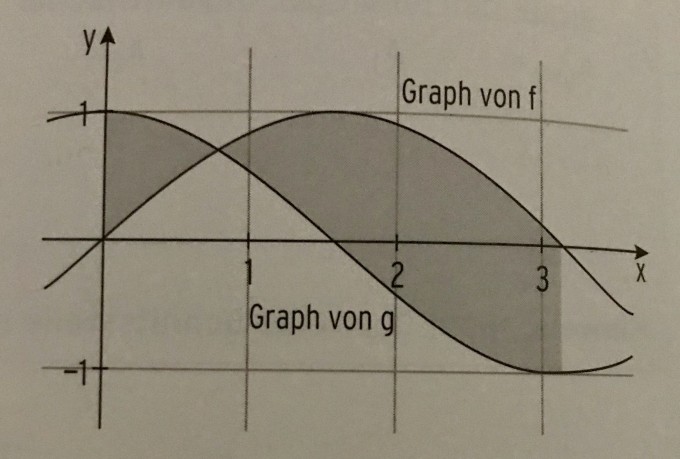
Die Funktionen f und g sind durch f(x)=sin(x) und g(x)=cos(x) gegeben. Wie groß ist die markierte Fläche? (S.Bild unten)

Könnt ihr mir bitte paar Tipps geben? :)

Answer 1

d(x) = COS(x) - SIN(x)

D(x) = COS(x) + SIN(x)

∫ (0 bis pi/4) d(x) dx = √2 - 1

∫ (pi/4 bis pi) d(x) dx = - √2 - 1 --> √2 + 1

A = √2 - 1 + √2 + 1 = 2·√2

Kontrolle

https://www.wolframalpha.com/input/?i=integral_0%5Epi+%7Ccos(x)-sin(x)%7C+dx

Comments

f(x) = COS(x) - SIN(x)
widerspricht dem Aufgabentext :  besser d nennen.

Einfacher :  Symmetrie ausnutzen und nur noch das eine Integral
∫ (pi/4 bis pi/4+pi) d(x) dx  auswerten, dazu benötigt man lediglich, dass die y-Werte der Schnittpunkte ±1/√2 sind.

---

@Gast hj2166

Danke für die Anmerkung.

Ich habe f(x) in d(x) geändert. Auf betrachtung der Symmetrie hatte ich bewusst verzichtet. Wenn der Fragesteller die Symmetrie kennt, darf er die aber gerne anwenden.

Ansonsten hätte er nur nachgefragt warum das so ist.