Falls die Sachlage so ist.
Die Seitenlängen der Quadrate verkürzen sich dabei bei
jedem Schritt um ein Viertel.
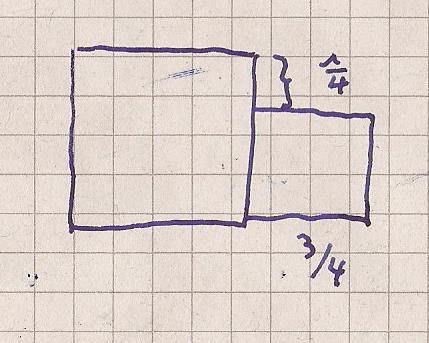
Unendliche geometrische Reihe
Trittfläche
sn - 3/4 * sn = 1
1/4 * sn = 1
sn = 4
Seitenlänge Quadrat 0.5 m
Länge = 0.5 * 4 = 2 m
Spiegelfläche
sn - 1/4 * sn = 1
3/4 * sn = 1
sn = 4/3
Länge = 0.5 * 4/3 = 0.67 m
Gesamtlänge
2 + 0.67 = 2.67 m