Eine Literatur empfehlung nehme ich auch dankend entgegen!
Inzwischen gibt es einen Wikipedia-Artikel zum Thema, der auch IMHO so gut ist, dass man den Algorithmus leicht nachvollziehen kann (2013 war das noch nicht so!). An Hand der in der Frage gegebenen Funktion kann man auch gut zeigen, wie er abläuft. Ich habe dafür ein C++-Programm geschrieben (s.u.) und habe versucht den Ablauf mit Geoknecht3D zu visualisieren:
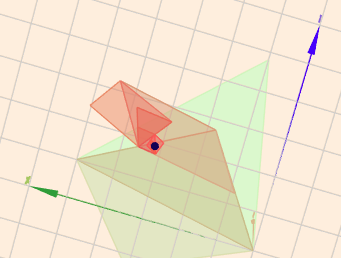
Die Funktion \(f(x,y) = x^{2} - 4x + y^{2} - y - xy\) hat bekanntermaßen (s. Antwort von Moliets) ein Minimum bei \((3|\,2)\), was ich oben als Punkt markiert habe. Jeder Iterationsschritt besteht aus drei Punkten, die ich als Dreieck dargestellt habe, die sich im Verlauf immer weiter um dieses Optimum zuziehen. Im Laufe der Iterationen färben sich die Dreiecke von hellgrün bis dunkelrot.
Hier noch ein Beispiel ...
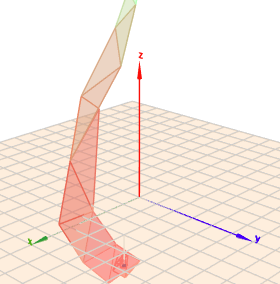
... bei dem ich das 'Startdreieck' abseits des Optimums gesetzt habe. Man kann sehr schön sehen, wie sich der Algorithmus Richtung Optimum bewegt und es schließlich auch 'einkreist'.
Das Programm:
// -- Beispiel für den Downhill Simplex Algorithmus in C++
#include <algorithm>
#include <numeric>
#include <iostream>
#include <vector>
using xi_type = CVector;
// -- liefert diese Funktion 'true', so bricht der Algorithmus ab
bool genau_genug( const std::vector< xi_type >& xi )
{
using std::abs;
auto u = xi[1] - xi[0];
auto v = xi[2] - xi[0];
auto w = xi[1] - xi[2];
return abs(u)*abs(v)*abs(w)/(2*abs(u % v)) <= 0.1; // -> Umkreisradius <= 1/10
}
int main()
{
using namespace std;
auto const alpha = 1.;
auto const beta = 0.5;
auto const gamma = 2.;
auto const sigma = 0.5;
// -- die zu optimierende Funktion aus https://www.mathelounge.de/54579
auto const func = []( const xi_type& p ) {
double x = X(p); double y = Y(p);
return x*x -x*y + y*y - 4*x - y;
};
// == das Startdreieck
vector< xi_type > xi = {xi_type(0,0), xi_type(5,1), xi_type(1,5) };
// vector< xi_type > xi = {xi_type(-4,-4), xi_type(-4,-4.5), xi_type(-4.5,-4.2) };
auto const N = size_t(xi.size()-1);
cout.precision(4);
auto farbe = CVector(0xb,0xf,0xb); // ... alles für den Farbverlauf
auto const t = 0.2;
auto Z_factor = 0.2;
auto const ist_besser = [func]( const xi_type& a, const xi_type& b ) {
return func(a) < func(b); // Vergleich: a ist besser als b, wenn func(a) < func(b)
};
int k=0;
for( ; !genau_genug(xi); ++k, farbe = t*CVector(0xf,0x4,0x4) + (1-t)*farbe)
{
cout << "dreieck("; // Ausgabe im Format für Geoknecht3D
for(auto x: xi)
cout << X(x) << "|" << Y(x) << "|" << func(x)*Z_factor << " ";
cout << ")" << gz::farbe(farbe) << endl;
// sortiere die Punkte: x[0] ist der beste, x[N] der schlechteste
sort( begin(xi), end(xi), ist_besser );
// m: Mittelpunkt der 'besseren' Punkte
auto m = accumulate( begin(xi), end(xi)-1, xi_type() ) / N;
// reflektiere den schlechtesten Punkt xi[N] am Mittelpunkt m, -> r
auto r = (1+alpha) * m - alpha * xi[N];
if( ist_besser(r, xi[0]) )
{ // wenn r beser als x[0], bestimme den expandierten Punkt e und ersetze x[N] durch
// den besseren von r und e
auto e = (1+gamma)*m - gamma*xi[N];
xi[N] = min( r, e, ist_besser );
continue;
}
if( ist_besser(r, xi[N-1]) )
{ // wenn r besser als der zweitschlechteste Punkt x[N-1] ist, ersetze x[N] durch r
xi[N] = r;
continue;
}
// sei h der bessere der beiden Punkte x[N] und r. Bestimme den
// kontrahierten Punkt c = (1+ß)m - ßh
auto h = min( r, xi[N], ist_besser );
auto c = (1+beta) * m - beta * h;
if( ist_besser(c, xi[N]) )
{ // wenn c besser als x[N] ersetze x[N] durch c
xi[N] = c;
continue;
}
for( auto& x: xi ) // komprimiere den Simplex in Richtung des besten Punktes x[0]
x = sigma * xi[0] + (1. - sigma) * x;
}
cout << "punkt(3|2|" << func(xi_type(3,2))*Z_factor << ")" << endl; // für Geoknecht3D
auto opt = *min_element( begin(xi), end(xi), ist_besser );
cout.precision(6);
cout << "Optimum[" << k << "]: x=" << X(opt) << " y=" << Y(opt)
<< " f(x,y)=" << func(opt) << endl;
return 0;
}