falls dir die Integrationsmethoden nicht geläufig genug sind, bzw. du die dabei benutzten Funktionstypen nicht verwendet hattest, oder andere Gründe, kannst du das ganze auch näherungsweise mit numerischen Verfahren lösen. Ich habe hier mal zwei verschiedene Verfahren aufgeführt, bei dem man schon recht nahe an das Ergebnis kommt.
Trapezmethode
$$ \int_a^bf(x)dx\approx\frac{f(a)+f(b)}{2}\cdot \frac{b-a}{n}+ \frac{b-a}{n}\cdot\sum_{k=1}^{n-1}{f\Big(a+k\cdot\frac{b-a}{n}\Big)} $$
a : Untergrenze, hier 0
b : Obergrenze, hier 820
n : äquidistante Zerlegung des Intervalls, hier [0,820] mit n=10
Dann hat man also:
$$ \int_0^{820}{\sqrt{1+\Big(\frac{14}{42025}x-\frac{56}{205} \Big)^2}}dx\approx \frac{f(0)+f(820)}{2}\cdot \frac{820-0}{10}+ \frac{820-0}{10}\cdot\sum_{k=1}^{10-1}{f\Big(0+k\cdot\frac{820-0}{10}\Big)}\\ \approx \frac{1,0366+1}{2}\cdot 82+ 82\cdot\sum_{k=1}^{9}{f(82k)}\\=83,5006+82\cdot\sum_{k=1}^{9}{f(82k)}\\=83,5006+82(f(82)+f(164)+f(246)+f(328)+f(410)+f(492)+f(574)+f(656)+f(738))\\=83,5006+82\cdot\sum_{k=1}^{9}{f(82k)}\\=83,5006+82(1,03+1,0236+1,0181+1,0133+1,0093+1,0060+1,0034+1,0015+1,0004)\\=\underline{\underline{830,1598}}$$
Oder direkt mit dem Computer berechnen lassen
Man berechnet es mit einem Computer direkt, auch nur numerisch, nach dieser Abbildung:
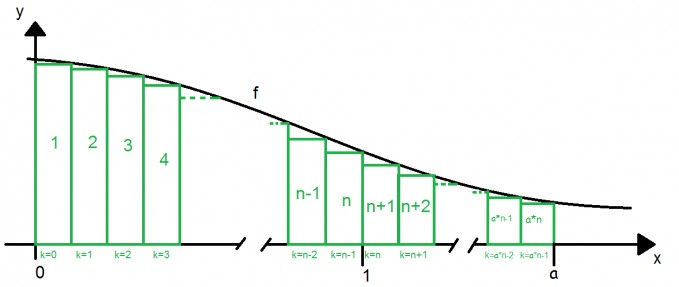
$$A_k=\frac{1}{n}\cdot f(x),\text{ mit } x:=\frac{k}{n} $$
Dann hat man:
$$ \sum_{k=0}^{a\cdot n-1}{A_k}=\sum_{k=0}^{a\cdot n-1}{\frac{1}{n}\cdot f\Bigg(\frac{k}{n}\Bigg)}=\frac{1}{n}\cdot\sum_{k=0}^{a\cdot n-1}{ f\Bigg(\frac{k}{n}\Bigg)} $$
$$\int_0^{820}{\sqrt{1+\Big(\frac{14}{42025}x-\frac{56}{205} \Big)^2}}dx\\[15pt]\stackrel{n=1000}{\approx}\frac{1}{1000}\cdot\sum_{k=0}^{820\cdot1000-1}{\sqrt{1+\Big(\frac{14}{42025}\cdot \frac{k}{1000}-\frac{56}{205} \Big)^2}}\approx \underline{\underline{830,0872}}$$
Python-Code:
from math import*
n = int(input(' n = ')) #Einteilungsschritte
a = float(input(' a = ')) #Obergrenze
summe = 0
k=0 #Laufvariable k
while k<=a*n-1: #Es wird solange aufaddiert, bis diese Bedingung nicht mehr gilt
summe = summe+sqrt(1+((14/42025)*(k/1000)-(56/205))**2)
k = k+1
print(summe/n)
