Ich bin am verzweifeln, ich verstehe einfach nicht, wie ich diese Aufgabe lösen soll...
vielleicht beginnst Du mit einer Zeichnung. Zeichne alles ein, was die Aufgabenstellung hergibt.
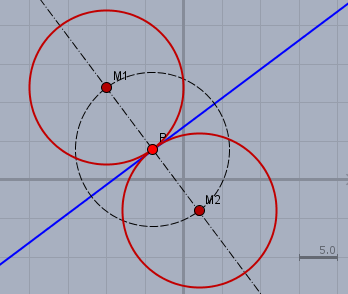
Die blaue Gerade ist die Gerade \(g\). Der Punkt \(P\) liegt auf der Geraden \(g\) und hat lt. Aufgabenstellung die Y-Koordinate \(4\). Also ist seine X-Koordinate
$$-3x+4y=28 \quad \Rightarrow x = \frac{28 - 4y}{-3} \quad \Rightarrow x(y=4)=-4$$ Der Punkt \(P\) hat also die Koordinate \(P(-4|4)\).
Die Mittelpunkte der gesuchten Kreise müssen auf einer Geraden liegen, die durch \(P\) verläuft und senkrecht auf \(g\) steht. Schreibt man \(g\) in der Vektorform
$$g: \space \begin{pmatrix} -3 \\ 4\end{pmatrix} \cdot \begin{pmatrix} x \\ y\end{pmatrix} = 28$$ so erhält man mit
$$n = \begin{pmatrix} -3 \\ 4\end{pmatrix}$$ bereits einen Vektor der senkrecht auf \(g\) steht. Zufällig hat er auch die Länge von 5, da \(\sqrt{4^2+3^2}=5= r/2\). Mann muss also nur zu \(P\) das doppelte des Vektor \(n\) addieren und für den zweiten Punkt das gleiche subtrahieren, um zu den Mittelpunkten der gesuchten Kreise zu kommen.
$$M_1= P + n = \begin{pmatrix} -4 \\ 4\end{pmatrix} + 2\begin{pmatrix} -3 \\ 4\end{pmatrix} = \begin{pmatrix} -10 \\ 12\end{pmatrix}$$
$$M_2= P - n = \begin{pmatrix} -4 \\ 4\end{pmatrix} - 2\begin{pmatrix} -3 \\ 4\end{pmatrix} = \begin{pmatrix} 2 \\ -4\end{pmatrix}$$ und wenn man jetzt noch weiß, wie eine Kreisgleichung aussieht, kann man diese unmittelbar hinschreiben. Es ist (in Vektorschreibweise)
$$k_1: \space (M_1 - x)^2 = r^2$$
und in Koordinatenform
$$k_1: (-10 - x)^2 + (12 - y)^2 = r^2=100$$
\(k_2\) schaffst Du jetzt alleine. Falls noch Fragen offen sind, so melde Dich bitte.
Gruß Werner
