Differentialgleichung inhomogene Gleichung kürzen

Question

ich habe folgende Differentialgleichung

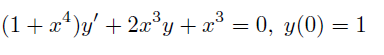
Umgestellt:

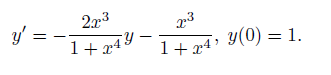
Lösung der Homogenen Gleichung

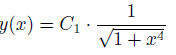
Mein Folgendes Problem liegt in der Bestimmung von der inhomogenen Gleichung bzw. in c(x) bestimmen

c(x)  =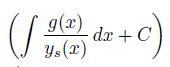 

Ich habe nun c(x) = Integral (-x^3/1+x^4) / (1 / sqrt(1+x^4)) dx + C

Habe es umgeschrieben zu

c(x) = Integral (-x^3 * sqrt(1+x^4)) / (1* (1+x^4) dx + C

Die Lösung sagt folgendes

c(x) =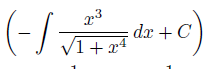 

Aber wie kürze ich nun g(x) / y_s(x) so das dass Ergebnis von der Lösung raus kommt?

Über eine Antwort würde ich mich sehr freuen.

Euer Max.

Answer 1

habs auch mit "Variation der Konstanten" gerechnet, obwohl nicht nötig:

diese Aufgabe kannst Du auch mit Trennung d. Variablen lösen.

(1+x^4) y' +2x^3 y+x^3=0

(1+x^4) y' +x^3(2y+1) =0

(1+x^4) y' =  - x^3(2y+1)

(1+x^4) dy/dx =  - x^3(2y+1) |*dx

(1+x^4) dy =  - x^3(2y+1) dx

dy/(2y+1) = (-(x^3 dx)/(1+x^4)

usw.

Comments

Vielen Dank für die ausführliche Antwort. Hat mir weitergeholfen! :)