ich habe die Differentialgleichung
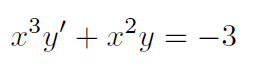
Ich stelle die Differentialgleichung erstmal um nach:
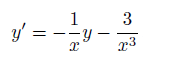
f(x) = - 1/ x ; g(x) = -3 / x^3
Nun gibt es zwei Möglichkeiten die Homogene Gleichung zu lösen.
1. Laut Formel
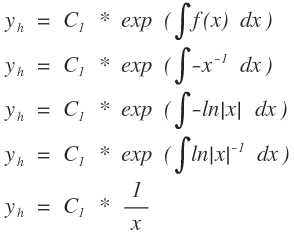
2. So wie ich die Homogene Gleichung zur Zeit lösen kann
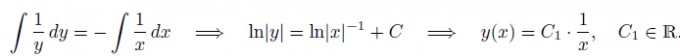
Ich verwende immer 2. "So wie ich die Homogene Gleichung zur Zeit lösen kann". Ist dies richtige oder sollte ich lieber die Formel verwenden?
Nun kommt die Lösung der inhomogenen Gleichung
-------------------------
Dazu gibt es folgende Formel bzw. weitere Schritte:
Schritt 2: Ersetze die Integrationskonstante C1 durch eine zu bestimmende
Funktion c(x) und mache den Lösungsansatz
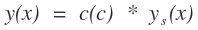
Schritt 3: Setze den Lösungsansatz in die inhomogene DGL ein und bestimme
c(x) aus der resultierenden DGL für die Funktion c
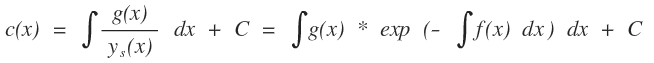
Daraus ergibt sich die allgemeine Lösung für die inhomogene DGL
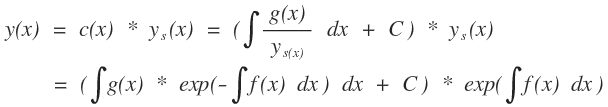
-------------------------
Nun mache ich den 3. Schritt:
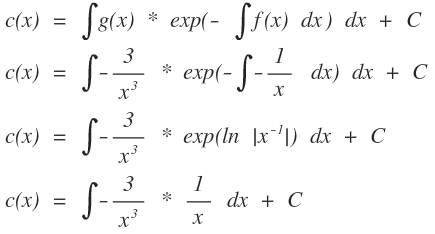
Ich habe das nun soweit geschrieben, muss ich nun * 1 / x auch nochmal integrieren oder so lassen bzw. vor dem Integral vorziehen?
Und wenn ich das nun habe, wie gehe ich weiter voran?
Über eine Antwort würde ich mich freuen.
Max Fischer