Normalerweise verwendet man ja folgende Tabelle, um Perzentilen WS zuzuordnen und umgekehrt:
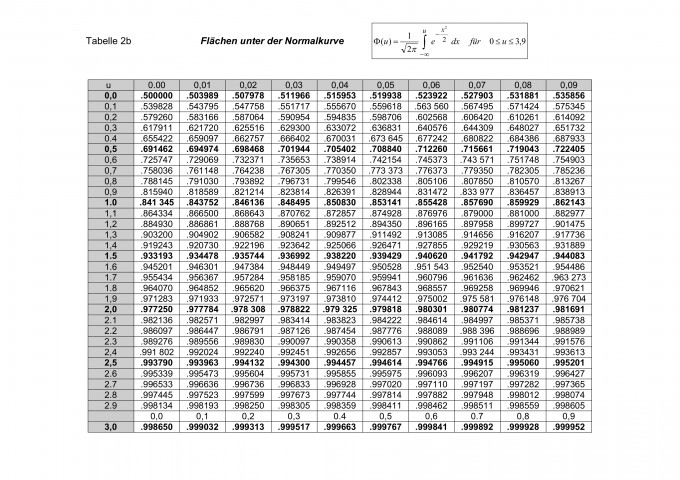
Nun bearbeite ich eine Aufgabe in der das 10% Quantil errechnet werden muss.
In einer Klinik wird eine Studie zum Gesundheitszustand von Frühgeburten durchgefhürt. Das Geburtsgewicht x eines in der 28. Schwangerschaftswoche geborenen Kindes wird als normalverteilte Zufallsvariable mit Erwartungswert 1000 g und Standardabweichung 50 g angenommen.
b) Bestimmen Sie das \( 10 \% \) - Quantil des Geburtsgewichts. \(1026.99 \)
Ich habe dafür auf diese Tabelle zurück gegriffen, was anscheinend falsch war. In der Auflösung steht dann folgendes.
b) Ein möglicher Lösungsweg lautet:
\( P(X \leq a)=0,1 \)
\( P\left(Z \leq \frac{a-\mu}{\sigma}\right)=0,1 \)
\( \left(\frac{a-\mu}{\sigma}\right)=z_{0,1} \)
\( \boldsymbol{a}=\boldsymbol{z}_{0,1} \cdot \boldsymbol{\sigma}+\boldsymbol{\mu} \)
\( a=-1,28 \cdot 50 g+1000 g \)
\( a=936 g \)
Anstelle von u0,1 ist nun von z0,1 die Rede und die passende WS stimmt entsprechend nicht.
Also was ist der Unterschied von Perzentil z zu Perzentil u und wie erhält man dessen Wert (hier -1,28)?