Aufgabe
f(x) = -1/540 x^{4} + 1/81 x^{2} + 32/9
g(x) = 1/27 x^{2}
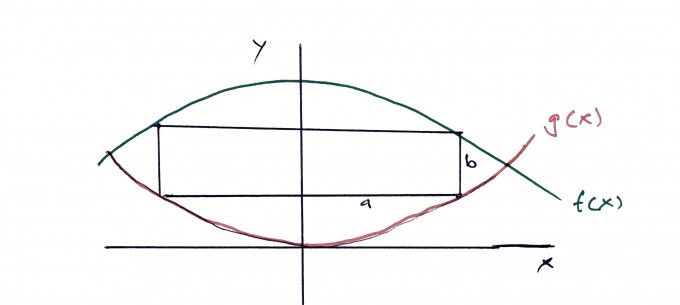
Der Hersteller dieses Rechteckmoduls benötigt die genaue Länge 2a des Rechtecks so, dass der Flächeninhalt maximal wird.
(Ohne Berechnung der 2. Ableitung). Die Längeneinheit is Meter.
Gesucht ist also A_(max) = a * b
Problem
b lässt sich so ausdrücken:
b = f(b) - g(b)
a = ?