Unterschied von Funktion und Nicht-funktion

Question

Was unterscheidet eine Funktion von einer nicht-Funktion? Und wie kann man diesen Unterschied auch in einem Diagramm erkennen?

Answer 1

Sobald im Koordinatensystem zwei Punkte des Graphen exakt vertikal übereinanderliegen, ist es keine Funktion mehr.

Grund: Dem x-Wert auf der Verbindung der beiden Punkte werden 2 Werte zugeordnet. Das ist gemäss Definition von 'Funktion' verboten.

Definition von Funktion. vgl. z.B. von https://www.wolframalpha.com/input/?i=function&a=*C.function-_*MathWorld-

Also: Eine Funktion ist eine Relation (Zuordnung), die jedem Element einer Menge eindeutig ein Element einer andern Menge zuordnet.

Comments

Kannst du das noch anders formulieren? tut mir leid aber ich hab das jetzt nicht verstanden /:

---

Wie genau lautet denn die Definition von 'Funktion' in deinen Unterlagen?

---

Also wir haben einen zettel bekommen und da stand :

Ich weiß, was eine Funktion von einer nicht-funktion unterscheidet und kann diesen Unterschied auch in einem Diagramm erkennen.


Aber das weiß ich nicht und deswegen suche ich eine gute erklärung :(

---

Also meinst du das so? :

Sagen wir, zwei punkte eines graphen liegen übereinander. z.B. A (1/2) und B (1/4)

Wenn das so vorliegt ist es keine funktion also eine ´nicht-funktion´?

---

Das ist ja nur eine Frage nach deinen Kenntnissen. Wenn ihr den Begriff Funktion nicht im Unterricht oder in den Unterlagen behandelt habt, schriebst du als Antwort besser nein. Da kann dir das die Lehrperson an deine Schulstufe angepasst noch beibringen.

Ich hab dir die mathematische Definition von Funktion oben schon gegeben. Aus ihr ergeben sich die geometrischen Eigenschaften ihrer Graphen.

HIer mal eine Skizze:

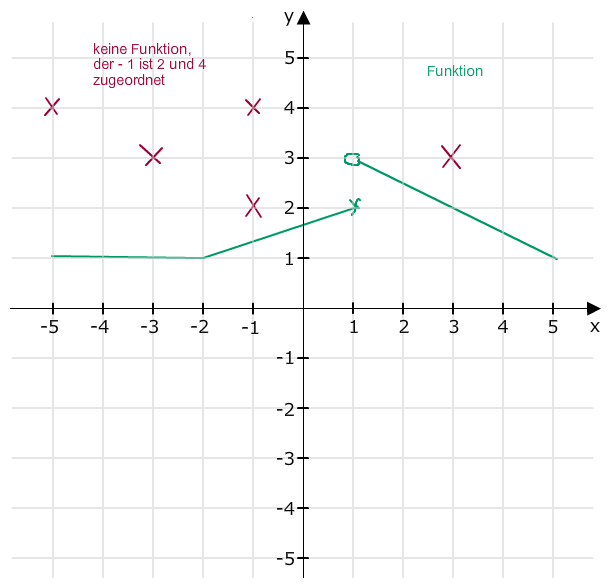
Die roten Punkte können nicht den Graph einer Funktion bilden, da

-1 → 2

und gleichzeitig

-1 → 4

Grün kann der Graph einer Funktion sein, da den x-Werten immer nur ein y-Wert zugeordnet wird.

Bei 1 → 2 und nicht auch noch die 3 (deshalb dort der Kreis)

---

Richtig. Du hast das gut formuliert. Es ist dann keine Funktion; nicht unbedingt die  ''Nicht-Funktion''.

---

Okay, dankeschön du hast mir sehr geholfen! :-)

Answer 2

die Nichtfunktion ist eine spezielle Funktion: Sie bildet einen logischen Zustand auf sein Komplement ab:

\( A \mapsto N(A) = \bar A \).

Eine spezielle Instanz dieser Funktionenklasse besteht in der Nicht-Funktion auf der Zustandsmenge {0, 1}:

\( N(0) \equiv 1 \) und \( N(1) \equiv 0 \).

MfG

Mister