Betragsungleichung |4x−1|≥6 lösen - sind meine Ergebnisse richtig?

Question

folgende Ungleichung soll gelöst werden:

|4x−1|≥6

1. Fall:

4x−1≥6 --> x ≥ -1,75

2. Fall:

−4x+1≥6 --> x< 0,8

Stimmt das denn so?

Answer 1

|4x−1|≥6

https://www.wolframalpha.com/input/?i=%7C4x−1%7C≥6

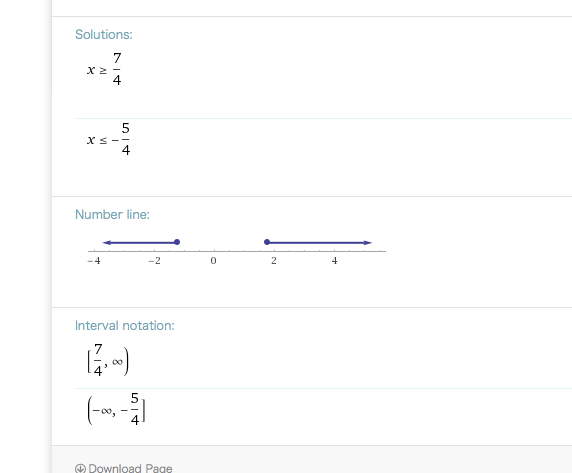
Du musst bei deinen Fällen noch Bedingungen hinzufügen und kommst so gelegentlich auf zwei Intervalle, die zu vereinigen sind.

|4x−1|≥6

1. Fall: x≥1/4 

4x−1≥6 --> x ≥ 1,75

L_{1} = [1.75, unendlich)

2. Fall: x≤1/4

−4x+1 ≥ 6 --> -5 ≥ 4x

-1.25 ≥ x

L_{2) = (-unendlich, -1.25]

Insgesamt L = (-unendlich, -1.25] u [1.75, unendlich) 

Answer 2

1. Fall:

4x−1≥6 --> x ≥+1,75

2. Fall:

−4x+1≥6 --> x< - 1,2    

Answer 3

\( |4 x-1| \geq 6 \)
\( \sqrt{(4 x-1)^{2}} \geq\left. 6\right|^{2} \)
\( (4 x-1)^{2} \geq 36 \)
\( 16 x^{2}-8 x+1 \geq 36 \)
\( 16 x^{2}-8 x \geq 35 \)
\( x^{2}-\frac{1}{2} x \geq \frac{35}{16} \)
\( \left(x-\frac{1}{4}\right)^{2} \geq \frac{35}{16}+\frac{1}{16} \)
\( \left(x-\frac{1}{4}\right)^{2} \geq\left.\frac{36}{16}\right|^{\frac{1}{2}} \)
1.) \( x-\frac{1}{4} \geq \frac{6}{4} \)
\( x_{1} \geq \frac{7}{4} \)
2.) \( x-\frac{1}{4} \leq-\frac{6}{4} \)
\( x_{2} \leq-\frac{5}{4} \)