Den Trick mit der Determinante hast Du ja bereits hinreichend erklärt bekommen. Man kann sich dem Problem aber auch ganz anders annehmen. Dazu muss man wissen, dass eine Parabel der Ort aller Punkte ist, die von einem Brennpunkt \(F\) und einer Geraden - der sogenannten Leitline - gleich weit entfernt ist. Im Bild habe ich Leitlinie und Parabel blau eingezeichnet.
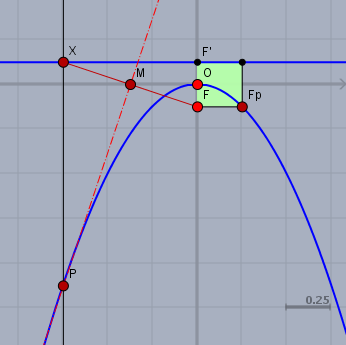
Bei einer gegebenen Parabel erhält man Brennpunkt und Leitlinie aus einem Quadrat (grün), dass durch folgende vier Punkte gebildet, wird. Dem Brennpunkt \(F\), einem Schnittpunkt \(F_p\) der Parallelen zur Leitlinie durch den Brennpunkt mit der Parabel und der beiden Projektionen der Punkte auf die Leitlinie. Bennene ich die X-Koordinate von \(F_p\) mit \(x_f\), dann muss hier gelten: $$f(x_f)=-2x_f^2 = \frac12 x_f \quad \Rightarrow x_f = - \frac14 $$ da der Abstand von \(F_p\) zu \(F\) lt. Definition (s.o.) genauso groß ist wie der Abstand zur Leitlinie und der Scheitelpunkt \(O\) der Parabel muss aus dem selben Grund genau in der Mitte zwischen \(F\) und der Leitlinie liegen. Damit liegt der Brennpunkt \(F\) und die Leitlinie \(l\) fest: $$F = \begin{pmatrix} 0 \\ x_f/2 \end{pmatrix} = \begin{pmatrix} 0 \\ -1/8 \end{pmatrix} \\ l: \space y= \frac{-x_f}{2} = \frac18$$ Nun muss man noch wissen, dass man einen Punkt \(P\) der Parabel konstruieren kann, indem man auf \(l\) einen Punkt \(X\) wählt und das Lot (schwarz) in \(X\) zu \(l\) mit der Mittelsenkrechte von \(XF\) (rot) in \(P\) schneidet. Die Mittelsenkrechte (rot Strich-Punkt) ist gleichzeitig die Tangente der Parabel in \(P\).
Wenn diese Tangente die Steigung \(m=3\) hat, dann muss auch das Verhältnis $$|F'X| \div |F'F| = 3 \div 1 $$ sein. Und da \(|F'F| = x_f = 1/4\) (s.o.), ist $$|F'X| = -x_p = 3 \cdot \frac14 = \frac34 \quad \Rightarrow P = \begin{pmatrix} -3/4\\ -9/8 \end{pmatrix}$$